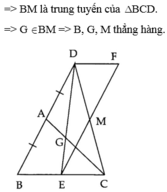
cho tam giác ABC,tia đối AB lấy D biết AD=AB.Lấy G thuộc AC biết AG=1/3 AC.Tia DG cắt BC=E.Qua E vẽ đường thẳng // với BD ,qua A vẽ đường thẳng // với BC, 2 đường thẳng này cắt nhau tại F.Gọi M là giao điểm của EF và CD.CMR B,G,M thẳng hàng

Những câu hỏi liên quan
cho tam giác ABC,tia đối AB lấy D biết AD=AB.Lấy G thuộc AC biết AG=1/3 AC.Tia DG cắt BC=E.Qua E vẽ đường thẳng // với BD ,qua A vẽ đường thẳng // với BC, 2 đường thẳng này cắt nhau tại F.Gọi M là giao điểm của EF và CD.CMR B,G,M thẳng hàng
Cần gấp :3
Cho ΔABC,trên tia đối của tia AB lấy điểm D sao cho AD=AB.Lấy G thuộc AC sao cho AG=1/3 AC.Tia DG cắt BC ở E.Qua E vẽ đường thẳng song song với BD.Qua D vẽ đường thẳng song song với BC,2 đường thẳng cắt nhau ở F.Gọi M là giao điểm của EF và CD. Cmr: CA,BM,DE đồng quy.
Cho tam giac ABC ,trên tia đối của cạnh AB lấy D(AD=AB).Lấy G thuộc AC(AG=1/3AC).Tia DG cắt BC ở E.Qua E kẻ đường thẳng song song với BD,qua D kẻ đường thẳng song song với BC ,hai đường này cắt nhau ở F.Gọi M là giao điểm của EF vàCD.C/m B,G,M thẳng hàng
Cho tam giác ABC, trên tia đối của AB lấy D sao cho AD=AB. Lấy G thuộc AC sao cho AG = 1/3.AC. Tia DG cắt BC tại E; qua E vẽ đường thẳng song song với BD; qua D vẽ đường thẳng song song với BC. Hai đường này cắt nhau tại F. Gọi M là giao của È và CD. Chứng minh 3 điểm B, G, M thẳng hàng.
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Lấy G thuộc cạnh AC sao cho AG = AC. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD. Chứng minh: a) G là trọng tâm tam giác BCD. b) , từ đó suy ra EC = DF
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD AB. Lấy G thuộc cạnh AC sao cho
A
G
1
3
A
C
. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.Chứng minh:a) G là trọng tâm tam giác BCD;b)
∆
B
E
D
∆...
Đọc tiếp
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Lấy G thuộc cạnh AC sao cho A G = 1 3 A C . Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.
Chứng minh:
a) G là trọng tâm tam giác BCD;
b) ∆ B E D = ∆ F D E , từ đó suy ra EC = DF;
c) ∆ D M F = ∆ C M E ;
d) B, G, M thẳng hàng.
cho tam giác,trên tia đối của AB lấy điểm D sao cho AB=AD.lấy G thuộc AC sao cho AG=1/3 AC.tia DG cắt BC ở E.Qua E vẽ đường song song với BD,qua D vẽ đường song song với BC,2 đường thẳng này cắ nhau ở F.
Chứng minh điểm B,G,M thẳng hàng
cho tam giác ABC trên tia đối của AB lấy D sao cho AD = AB . Lấy G thuộc AC sao cho AG =1/3 AC . Tia DG cắt BC tại E . Qua E vẽ đường thẳng song song với BD . Qua D vẽ dường thảng song song với BC 2 đường này cắt nhau tại F gọi M là giao điểm của EF vsf CD
a)chứng minh G là trọng tâm của tam giác BCD
b)chứng minh tam giác BED = tam giác FDE
Cho ∆ ABC . Trên tia đối của tia AB lấy D sao cho AD=AB.lấy G thuộc AC sao cho AG=1/3 AC. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD,qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD. Chứng minh rằng:
a)G là trong tâm của ∆ BCD.
b) ∆DMF =∆ CME