Vì đường thẳng (d) cắt Oy tại điểm có tung độ bằng 8

Nên m+3=8⇔ m=5

Theo pt hoành độ giao điểm của (d) và (P)

Ta có:\(x^2=2x+8\)

⇔\(x^2-2x-8=0\)

\(\Delta'=\left(-1\right)^2-\left(-8\right)=9\)

\(\sqrt{\Delta'}=\sqrt{9}=3>0\)

Vậy pt có 2 nghiệm pb

x₁₌\(\dfrac{1+3}{1}=4\)

x₂=\(\dfrac{1-3}{1}=-2\)

Với x =4 thì y=x²=4²=16

Với x =-2 thì y=x²=(-2)²=4

Vậy ......

Mọi người ơi giúp mình với😭

`m=1 => y=2x+1^2+9=2x+10`

Phương trình hoành độ giao điểm:

`x^2=2x+10`

`<=>x^2-2x-10=0`

`<=>` \(\left[{}\begin{matrix}x=1-\sqrt{11}\\x=1+\sqrt{11}\end{matrix}\right.\)

`=>` \(\left[{}\begin{matrix}y=12-2\sqrt{11}\\y=12+2\sqrt{11}\end{matrix}\right.\)

`=>` Tọa độ 2 giao điểm là: `(1-\sqrt11 ; 12-2\sqrt12) ; (1+\sqrt11 ; 12+2\sqrt11)`.

a) Khi \(m=1\) \(\Rightarrow\left(d\right):y=2x+8\)

Xét phương trình hoành độ giao điểm

  \(x^2=2x+8\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)

+) Với \(x=4\Rightarrow y=16\)

+) Với \(x=-2\Rightarrow y=4\)

  Vậy khi \(m=1\) thì (P) cắt (d) tại 2 điểm phân biệt \(\left(4;16\right)\) và \(\left(-2;4\right)\)

b) Xét phương trình hoành độ giao điểm

  \(x^2-2x+m^2-9=0\)  (*)

Ta có: \(\Delta'=10-m^2\) 

Để (P) cắt (d) \(\Leftrightarrow\) Phương trình (*) có 2 nghiệm phân biệt 

\(\Leftrightarrow\Delta'=10-m^2>0\) \(\Leftrightarrow-\sqrt{10}< m< \sqrt{10}\)

Theo đề: (P) cắt (d) tại 2 điểm nằm về 2 phía của trục tung

\(\Leftrightarrow\) Phương trình (*) có 2 nghiệm trái dấu

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\x_1x_2< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}10-m^2>0\\m^2-9< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{10}< m< \sqrt{10}\\-3< m< 3\end{matrix}\right.\) \(\Leftrightarrow-3< m< 3\)

  Vậy ...

`a)`

`@ O(0;0), A(1;1), B(-1;1) in (P)`

`@ C(0;2), D(-2;0) in (d)`

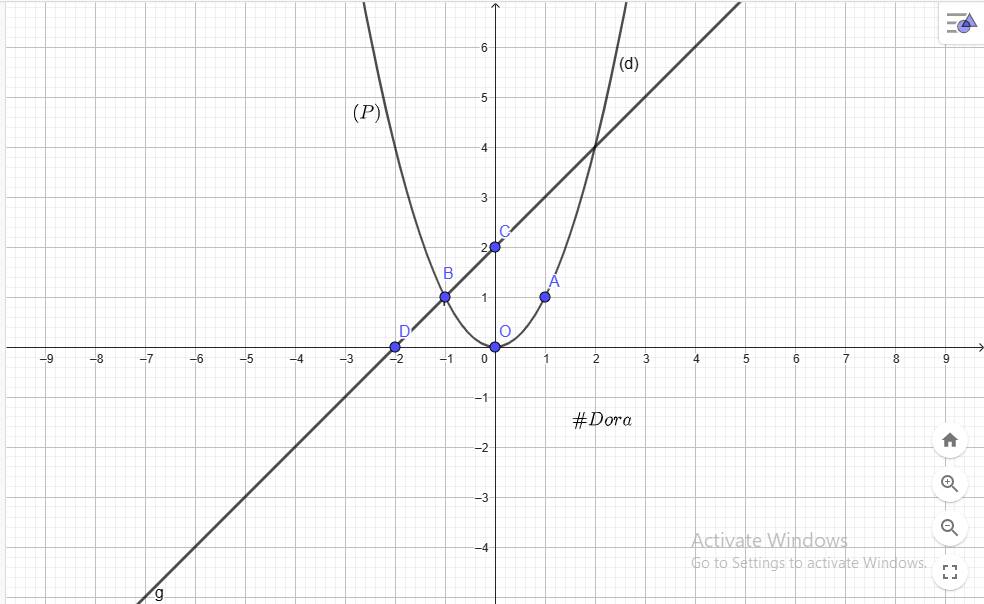
`b)` Ptr hoành độ của `(P)` và `(d)` là:

     `x^2=x+2`

`<=>x^2-x-2=0`

Ptr có: `a-b+c=1+1-2=0`

   `=>x_1=-1;x_2=-c/a=2`

  `=>y_1=1;y_2=4`

`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`

`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`

Thay `a=1;M(2;5)` vào `(d')` có:

         `5=2+b<=>b=3` (t/m)

  `=>` Ptr đường thẳng `(d'): y=x+3`