45x-38x=1505

=>7x=1505

=>x=215

X*(45-38)=1505

X*7=1505

X=1505:7

X=215

ủa sao m.n toàn giải hộ tui ko vậy,tui bảo nêu cách giải mà 😑

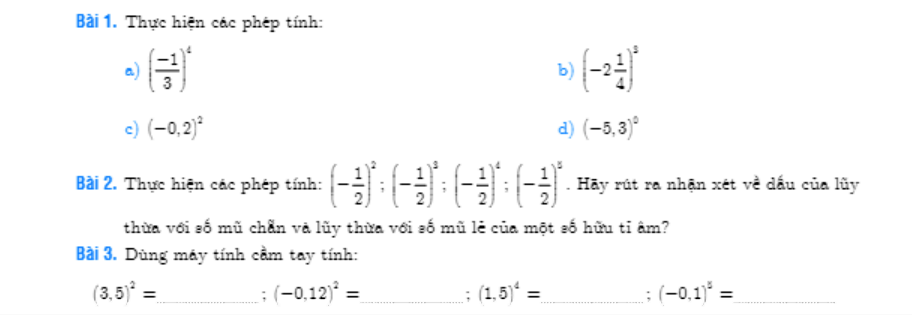
Bài 2: 

Lũy thừa với số mũ chẵn của một số hữu tỉ âm là số dương

Lũy thừa với số mũ lẻ của một số hữu tỉ âm là số âm

Bài 8:

a: \(2^{27}=8^9\)

\(3^{18}=9^9\)

Bài 13:

a: \(x^3=343\)

nên x=7

b: \(\left(2x-3\right)^2=9\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)

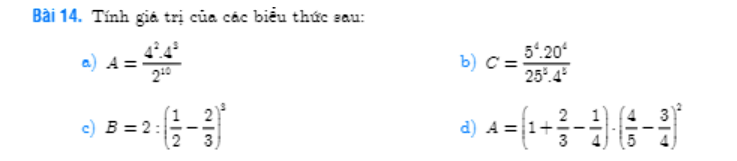
a: \(A=\dfrac{4^2\cdot4^3}{2^{10}}=\dfrac{4^5}{2^{10}}=1\)

b: \(C=\dfrac{5^4\cdot20^4}{25^5\cdot4^5}=\dfrac{100^4}{100^5}=\dfrac{1}{100}\)

Bài 9:
a: \(10^8\cdot2^8=20^8\)

b: \(10^8:2^8=5^8\)

c: \(25^4\cdot2^8=100^4\)

d: \(27^2:25^3=\left(\dfrac{9}{25}\right)^3\)

Bài 4: 

a: \(x:\left(-\dfrac{1}{2}\right)^3=-\dfrac{1}{2}\)

\(\Leftrightarrow x=\dfrac{-1}{2}\cdot\dfrac{-1}{8}\)

hay \(x=\dfrac{1}{16}\)

b: \(\left(\dfrac{3}{4}\right)^3\cdot x=\left(\dfrac{3}{4}\right)^7\)

\(\Leftrightarrow x=\left(\dfrac{3}{4}\right)^7:\left(\dfrac{3}{4}\right)^3=\left(\dfrac{3}{4}\right)^4=\dfrac{81}{256}\)

Mọi người làm giúp mình với nha

34 : B

35 : D

36 : A

37 : A

38: C

39: B

4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).

Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)

\(\Rightarrow xy+yz+zx=-1\).

Bất đẳng thức đã cho tương đương:

\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).

Vậy ta có đpcm

mình xí câu 45,47,51 :>

45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :

\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)

Đẳng thức xảy ra <=> a=b

b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)

\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)

\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)

Cộng (1),(2),(3) theo vế ta có đpcm

Đẳng thức xảy ra <=> a=b=c

47. Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :

\(\dfrac{\left(a+b\right)^2}{c}+\dfrac{\left(b+c\right)^2}{a}+\dfrac{\left(c+a\right)^2}{b}\ge\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+c}=\dfrac{\left[2\left(a+b+c\right)\right]^2}{a+b+c}=\dfrac{4\left(a+b+c\right)^2}{a+b+c}=4\left(a+b+c\right)\)(đpcm)

Đẳng thức xảy ra <=> a=b=c