a) 2x2 - x + 2 chia hết cho 2x + 1
b)3x3 + 4x2 - 5chia hết cho x -1
Mình xin cảm ơn!
Những câu hỏi liên quan
5x-16=40+x
5x-7=-21-2x
3:chia hết cho x
-5chia hết cho x-1
6 chia hết cho 2x-1
làm giúp mk với mk cảm ơn
\(5x-16=40+x\)
\(\Leftrightarrow5x=40+x+16\)
\(\Leftrightarrow5x=x+56\)
\(\Leftrightarrow5x-x=56\)
\(\Leftrightarrow4x=56\)
\(\Leftrightarrow x=14\)
Vậy \(x=14\)
\(5x-7=-21-2x\)
\(\Leftrightarrow5x-7+21=-2x\)
\(\Leftrightarrow5x+14=-2x\)
\(\Leftrightarrow-2x-5x=14\)
\(\Leftrightarrow-7x=14\)
\(\Leftrightarrow x=-2\)
Vậy \(x=-2\)
29 tháng 10 2021 lúc 19:00
Bài 1 : Tìm a để (5x3 - 3x2 + 2x +a) chia hết cho ( x +1)Bài 2 : Tìm a để phép chia sau là phép chia hết :a) ( x3 - x2 + 2x + a) chia hết cho x -1b) x3 -2x2 -2x + a chia hết cho x +1Bài 3 Tìm các giá trị a , b ,k để đa thức f(x) chia hết cho đa thức g(x)a) f(x) x4 -9x3 + 21x2 + x +k ; g (x) x2 - x -2b) f(x) x4 - 3x3 + 3x2 + ax + b ; g(x) x2 - 3x +4
Đọc tiếp
Bài 1 : Tìm a để (5x3 - 3x2 + 2x +a) chia hết cho ( x +1)
Bài 2 : Tìm a để phép chia sau là phép chia hết :
a) ( x3 - x2 + 2x + a) chia hết cho x -1
b) x3 -2x2 -2x + a chia hết cho x +1
Bài 3 Tìm các giá trị a , b ,k để đa thức f(x) chia hết cho đa thức g(x)
a) f(x)= x4 -9x3 + 21x2 + x +k ; g (x) = x2 - x -2
b) f(x) = x4 - 3x3 + 3x2 + ax + b ; g(x) = x2 - 3x +4
Bài 1:
Ta có: \(5x^3-3x^2+2x+a⋮x+1\)
\(\Leftrightarrow5x^3+5x^2-8x^2-8x+10x+10+a-10⋮x+1\)
\(\Leftrightarrow a-10=0\)
hay a=10
Đúng 0
Bình luận (0)
a) tìm a để đa thức 4x3 - 2x2+ a chia hết cho đa thức 2x - 3
b) Tìm giá trị a để đa thức 3x3 + 2x2 + x + a chia cho đa thức x + 1 có số dư bằng 2
\(a,\Leftrightarrow4x^3-2x^2+a=\left(2x-3\right).a\left(x\right)\)
Thay \(x=\dfrac{3}{2}\Leftrightarrow4.\dfrac{27}{8}-2.\dfrac{9}{4}+a=0\)
\(\Leftrightarrow\dfrac{27}{2}-\dfrac{9}{2}+a=0\\ \Leftrightarrow a=-9\)
\(b,\Leftrightarrow3x^3+2x^2+x+a=\left(x+1\right).b\left(x\right)+2\)
Thay \(x=-1\Leftrightarrow-3+2-1+a=2\Leftrightarrow a=4\)
Đúng 1
Bình luận (1)
Bài 2: Tìm a,b để :
a. Đa thức 3x^3 + 2x2 -7x + a chia hết cho đa thức 3x-1b. ax^2 + 5x^4 chia hết cho (x-1)^2c. Đa thức 2x^2 + ã +1 chia x-3 được d là 4d. 2x^3 - x^2 + ax + b chia hết cho x^2 -1Hộ ak
a: 3x^3+2x^2-7x+a chia hêt cho 3x-1
=>3x^3-x^2+3x^2-x-6x+2+a-2 chia hết cho 3x-1
=>a-2=0
=>a=2
c: =>2x^2-6x+(a+6)x-3a-18+3a+19 chia x-3 dư 4
=>3a+19=4
=>3a=-15
=>a=-5
d: 2x^3-x^2+ax+b chiahêt cho x^2-1
=>2x^3-2x-x^2+1+(a+2)x+b-1 chia hết cho x^2-1
=>a+2=0 và b-1=0
=>a=-2 và b=1
Đúng 0
Bình luận (0)
Cho các khẳng định sau:(I): Phép chia đa thức
3
x
3
–
2
x
2
+ 5 cho đa thức 3x – 2 là phép chia hết(II): Phép chia đa thức (
2
x
3
+
5
x
2
– 2x + 3) cho đa thức (
2
x
2
– x + 1) là phép chia hếtChọn câu...
Đọc tiếp
Cho các khẳng định sau:
(I): Phép chia đa thức 3 x 3 – 2 x 2 + 5 cho đa thức 3x – 2 là phép chia hết
(II): Phép chia đa thức ( 2 x 3 + 5 x 2 – 2x + 3) cho đa thức ( 2 x 2 – x + 1) là phép chia hết
Chọn câu đúng
A. Cả (I) và (II) đều đúng
B. Cả (I) và (II) đều sai
C. (I) đúng, (II) sai
D. (I) sai, (II) đúng
Lời giải
Ta có
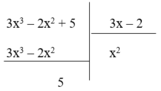
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3 x 3 – 2 x 2 + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai
Lại có
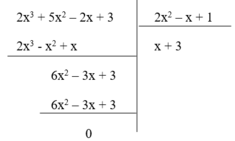
Nhận thấy phần dư R = 0 nên phép chia đa thức ( 2 x 3 + 5 x 2 – 2x + 3) cho đa thức (2 x 2 – x + 1) là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
1.Tìm số nguyên x
a,2x-5 chia hết cho x-1
b,3x+4 chia hết cho x-3
c,x-2 là ước của x2+8
2,Tìm x=Z
a,3x+2 chia hết cho x-1
b,x2+2x-7 chia hết cho x+2
3,Tìm cặp số nguyên x,y
a,(x-1).(y+1)=5
b,x.(y+2)= -8
Làm ơn mn giải nhanh giúp mình ngày mai mình phải nộp r!
Bài 1:
a: \(\Leftrightarrow x-1\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{2;0;4;-2\right\}\)
Đúng 1
Bình luận (0)
Tìm x thỏa mãn
a) 5chia hết cho x+1
b)x+5 chia hết cho x+2
c)2x+7 chia hết cho x+1
tim x;
a 63 chia hết cho (x-1)
b 14 chiia hết cho (2x+3)
c x+7chia hết cho x-1
d 2x+5chia hết cho x-2