giải dùm em 7.3 e cảm ơn rất nhiều

 giải gấp dùm mình với ạ. Mình cảm ơn các bạn rất nhiều
giải gấp dùm mình với ạ. Mình cảm ơn các bạn rất nhiều
giải dùm em s ạ
có gì giải thích dùm em luôn em cảm ơn nhiều

14.
\(y'=2x^3-4x=2x\left(x^2-2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
\(y''=6x-4\)
\(\Rightarrow y''\left(0\right)=-4< 0\Rightarrow x=0\) là điểm cực đại
\(y\left(0\right)=-3\)
\(\Rightarrow\) Điểm cực đại của đồ thị hàm số là \(\left(0;-3\right)\)
12.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(y''=6x\)
\(\Rightarrow\left\{{}\begin{matrix}y''\left(1\right)=6>0\\y''\left(-1\right)=-6< 0\end{matrix}\right.\) \(\Rightarrow x=-1\) là điểm cực đại
\(\Rightarrow\)Giá trị cực đại của hàm số là \(y\left(-1\right)=3\)
2.
\(y'=x^2-2mx+m^2-m+1\)
\(y''=2x-2m\)
Hàm đạt cực đại tại \(x=1\) khi:
\(\left\{{}\begin{matrix}y'\left(1\right)=0\\y''\left(1\right)< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m^2-3m+2=0\\2-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m>1\end{matrix}\right.\) \(\Rightarrow m=2\)
Tính: \(\dfrac{1}{3}:\dfrac{7.5+7.3}{18.53-18.11}\)
CÁC BẠN GIẢI CHI TIẾT BÀI NÀY GIÚP MÌNH NHÉ! CẢM ƠN CÁC BẠN RẤT NHIỀU! 🤧🙏💖
\(=\dfrac{1}{3}:\dfrac{7\cdot\left(5+3\right)}{18\cdot\left(53-11\right)}\)
\(=\dfrac{1}{3}:\dfrac{7\cdot8}{18\cdot42}\)
\(=\dfrac{1}{3}:\dfrac{7\cdot2\cdot2\cdot2}{3\cdot3\cdot2\cdot2\cdot3\cdot7}\)
\(=\dfrac{1}{3}:\dfrac{2}{3\cdot3\cdot3}\)
\(=\dfrac{1}{3}\cdot\dfrac{27}{2}\)
\(=\dfrac{9}{2}\)
mọi người giải dùm em vs ạ bạn em nhờ em hỏi dùm
em cảm ơn nhiều
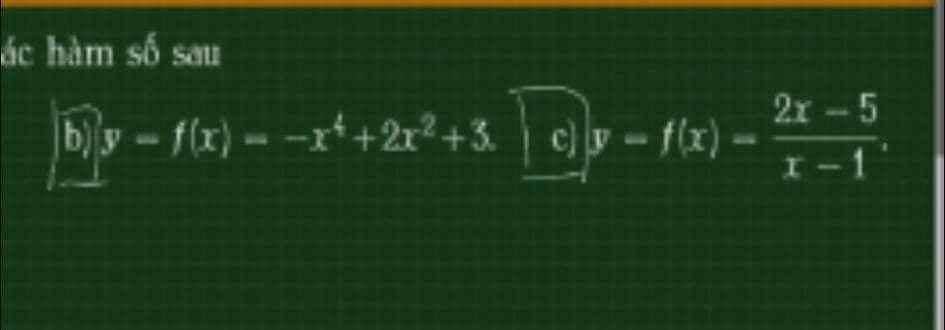

cái hồi nãy thiếu câu hỏi em bổ sung ở dưới này ạ
em cảm ơn mn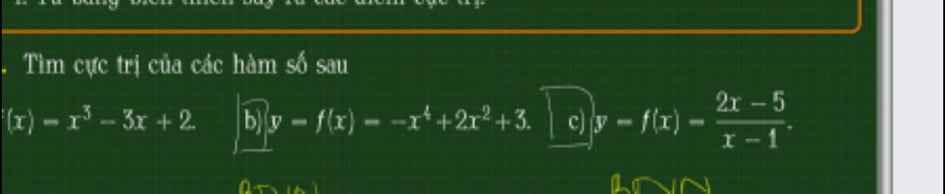
5.
TXĐ: \(D=\left(-\infty;-1\right)\cup\left(-1;+\infty\right)\)
\(y'=\dfrac{2}{\left(x+1\right)^2}>0\) ; \(\forall x\in D\)
\(\Rightarrow\) Hàm đồng biến trên mỗi khoảng xác định
Hay hàm đồng biến trên \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\)
6.
\(y=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu của y' trên trục số:
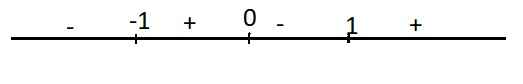
Từ đó ta thấy:
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Tìm cực trị
a.
\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
\(f''\left(x\right)=6x\)
\(f''\left(-1\right)=-6< 0\)
\(f''\left(1\right)=6>0\)
\(\Rightarrow x=-1\) là điểm cực đại và \(x=1\) là điểm cực tiểu
b.
\(f'\left(x\right)=-4x^3+4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
\(f''\left(x\right)=-12x^2+4\)
\(f''\left(0\right)=4>0\) ; \(f''\left(-1\right)=-8< 0\) ; \(f''\left(1\right)=-8< 0\)
\(\Rightarrow x=0\) là điểm cực tiểu và \(x=\pm1\) là 2 điểm cực đại
c.
\(f'\left(x\right)=\dfrac{3}{\left(x-1\right)^2}\ne0\) với mọi x thuộc miền xác định
Hàm không có cực trị
EM CẦN LỜI GIẢI CÂU NÀY Ạ. E CẢM ƠN RẤT NHIỀU

giải dùm em vs ạ em cảm ơn nhiều 
giải dùm em vs ạ em cảm ơn nhiều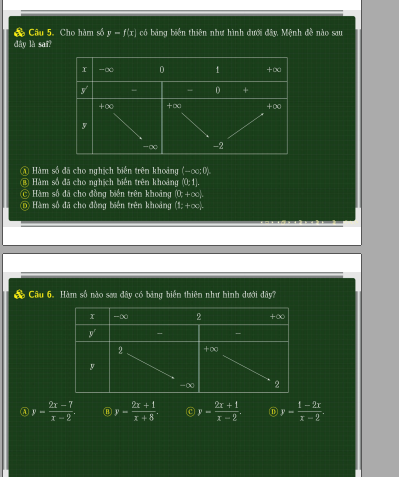
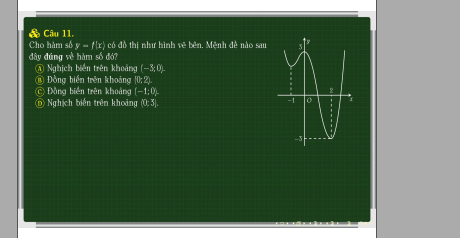


Câu 5:
Nhìn BBT trên \(\left(0;+\infty\right)\) ta thấy trên \(\left(0;1\right)\) đồ thị là đường đi xuống (nghịch biến) nên hàm đồng biến trên toàn miền \(\left(0;+\infty\right)\) là sai
Câu 6:
Từ BBT ta thấy hàm nghịch biến trên các khoảng xác định
\(\Rightarrow\) Loại 2 phương án A và B (ở 2 phương án này hàm đồng biến do y' lần lượt là \(\dfrac{3}{\left(x-2\right)^2}>0\) và \(\dfrac{15}{\left(x+8\right)^2}>0\))
Còn lại 2 phương án C và D, nhìn BBT ta thấy \(y=2\) là tiệm cận ngang (giá trị của y tại x vô cực)
\(\lim\limits_{x\rightarrow\infty}\dfrac{2x+1}{x-2}=2\) (đúng) nên chọn C
7.
Từ BBT ta thấy đây là BBT của hàm bậc 3 \(\Rightarrow\) loại B và D
Từ BBT, y'=0 có 2 nghiệm \(x=0,x=2\)
Ở đáp án A, \(y'=x^2+2x=0\Rightarrow x=0;x=-2\) (ktm)
Nên C đúng (\(y'=x^2-2x=0\Rightarrow x=0;2\))
11.
Nhìn đồ thị, ta thấy trên \(\left(-1;0\right)\) đồ thị chỉ có hướng đi lên \(\Rightarrow\) đồng biến trên (-1;0) nên C đúng
(A sai vì trên (-3;0) đồ thị có khoảng đi lên (đồng biến) ở (-1;0)
B sai vì trên (0;2) đồ thị đi xuống => nghịch biến chứ ko phải đồng biến
D sai vì trên (2;3) đồ thị đi lên (đồng biến)
5C, 6C, 7C, 11C
Cả 4 câu đều C luôn, kì quái thật
mọi người giải giúp em câu 71,74 với
em cảm ơn mọi người nhiều vẽ hình dùm em luôn em cảm ơn
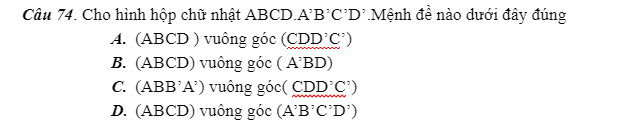
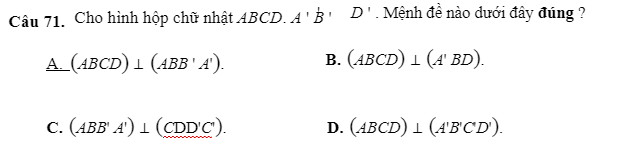
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
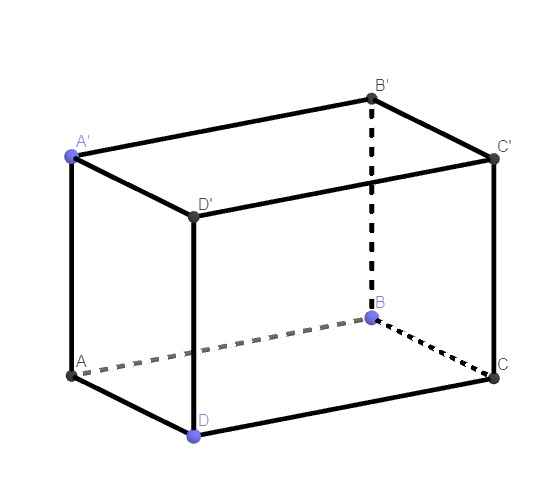
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)