chứng minh với b>0
a:neu a<b thi a/b<a+1/b+1
b:nếu a<b thì a/b>a+1/b+1
a) chứng minh a song song với b
b) chứng minh c vuông góc với b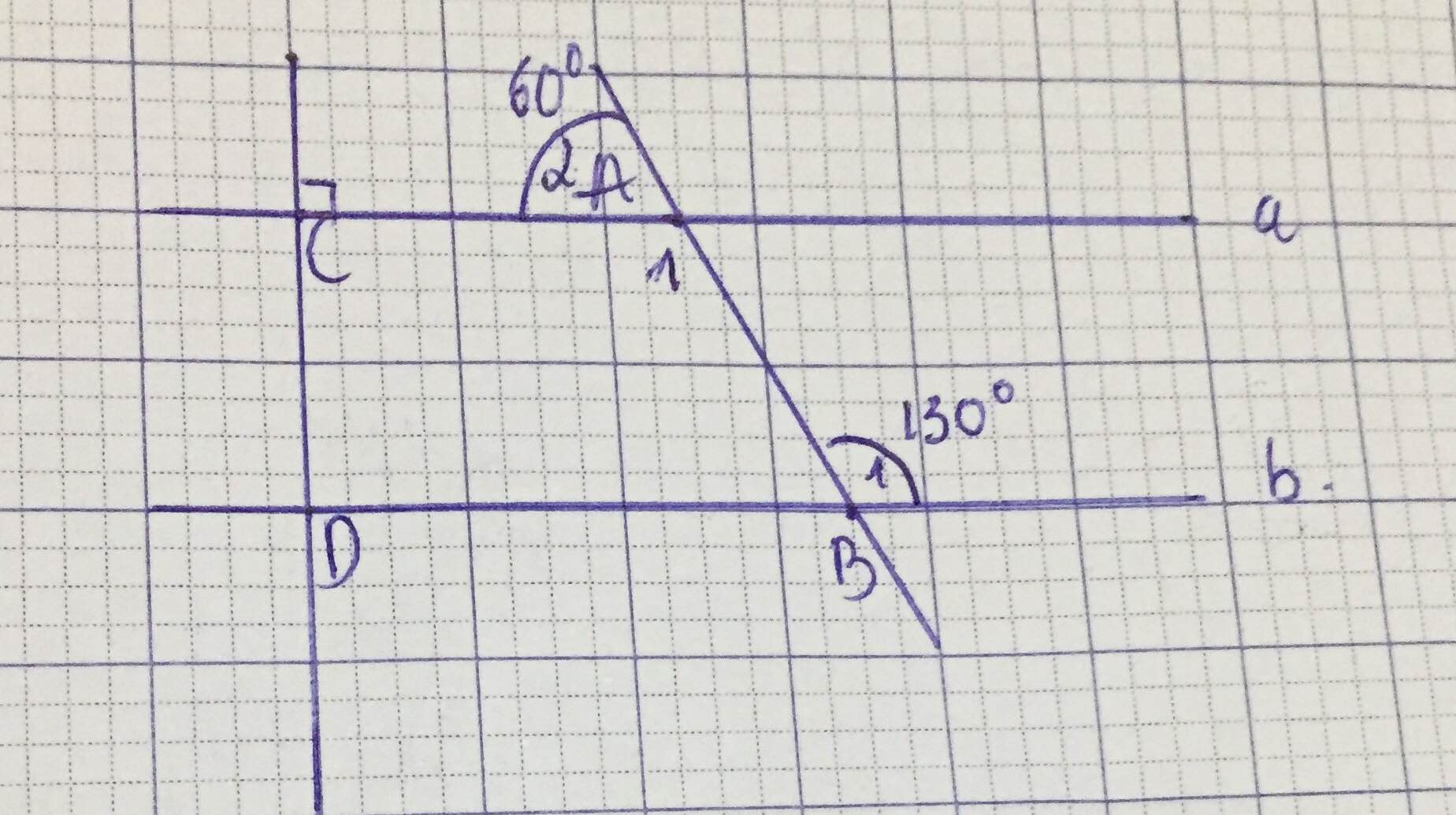
\(a,\) Muốn chứng minh \(a//b\) thì bạn phải sửa \(\widehat{B_1}=120\) nha
Ta có \(\widehat{A_1}+\widehat{A_2}=180\left(kề.bù\right)\Rightarrow\widehat{A_1}=180-\widehat{A_2}=120\)
Mà \(\widehat{B_1}=120\Rightarrow\widehat{A_1}=\widehat{B_1}\left(=120\right)\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow a//b\)
\(b,\left\{{}\begin{matrix}a\perp c\left(GT\right)\\a//b\left(cmt\right)\end{matrix}\right.\Rightarrow b\perp c\)
Cho a>2, b>2.
a) Chứng minh a.b > a+b
b) Chứng minh a^2+b^2+c^2 ≥ ab+bc+ca
c) Chứng minh a^2+b^2+c^2+3 ≥ 2.(a+b+c)
d) Chứng minh a^2+b^2 ≥ 1/2 với a+b=1
e) Chứng minh a^2+b^2+c^2 ≥ 1/3 với a+b+c=1
Bài 2: Cho ∆ABC cân tại A (𝐴̂ < 900 ). Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc với AB tại E .
a) Chứng minh ∆ADE cân ;
b) Chứng minh DE // BC;
c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC;
d) AI cắt BC tại K. Chứng minh AK vuông góc với BC.
Bài 3: Cho ∆ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD.
a) Chứng minh ∆BDE = ∆CED;
b) Chứng minh IB = IC, ID = IE;
c) Chứng minh DE // BC;
d) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng.
Bài 2:
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔADB=ΔAEC
Suy ra: AD=AE
hayΔADE cân tại A
b: Xét ΔABC có
AE/AB=AD/AC
nên DE//BC
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
EC=DB
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
=>AK là tia phân giác của góc BAC
Ta có: ΔABC cân tại A
mà AK là đường phân giác
nên AK là đường cao
Cho ∆ABC vuông tại A,kẻ phân giác BK của góc B(K thuộc AC),kẻ AF vuông góc với BK tại H và F thuộc BC A) chứng minh : ∆BHA=∆BHF B)chứng minh :FK vuông góc với BC C)chứng minh :AK
a) Vẽ MH vuông góc với AB, MK vuông góc với AC. Chứng minh AH=AK
b)Chứng minh HK // BC
a, Xét tam giác ABC cân tại A có AM là đường cao
đồng thời là đường phân giác
Xét tam giác AMH và tam giác AMK
AM _ chung
^MAH = ^MAK ( AM là phân giác )
Vậy tam giác AMH = tam giác AMK ( ch - gn )
=> AH = AK ( 2 cạnh tương ứng )
b, Ta có AH = AK ; AB = AC
=> HK // BC ( Ta lét đảo )
Xét \(\Delta AHM,\Delta AKM\) có:
\(\widehat{AHM}=\widehat{AKM}=90^o\)
\(\widehat{A_1}=\widehat{A_2}\)
\(AM:chung\)
\(\Rightarrow\Delta AHM=\Delta AKM\left(ch.gn\right)\)
\(\Rightarrow AH=AK\)
\(\Rightarrow\Delta AHK\) cân tại A
\(\Rightarrow\widehat{AHK}=\dfrac{180^o-\widehat{A}}{2}\left(1\right)\)
Vì \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ABC}=\dfrac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AHK}=\widehat{ABC}\)
Mà 2 góc này ở vị trí đồng vị
Suy ra \(HK//BC\)
1/Cho a > 2 | b | . Chứng minh rằng : | a | < 2 | a - b |
2/Chứng minh rằng : | a - c | < hoặc = | a - b | + | b - c | với a, b, c thuộc Z
GIÚP MÌNH VỚI, MÌNH RẤT CẦN
Bài 2:
Ta chứng minh \(\left|a+b\right|\le\left|a\right|+\left|b\right|\) (*) :
Bình phương 2 vế của (*) ta có:
\(\left(\left|a+b\right|\right)^2\le\left(\left|a\right|+\left|b\right|\right)^2\)
\(\Leftrightarrow a^2+b^2+2ab\le a^2+b^2+2\left|ab\right|\)
\(\Leftrightarrow ab\le\left|ab\right|\) (luôn đúng)
Áp dụng (*) vào bài toán ta có:
\(\left|a-c\right|\le\left|a-b+b-c\right|=\left|a-c\right|\) (luôn đúng)
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 =0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| < |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)
2 = 0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Cho tam giác ABC có AB = AC. M là trung điểm của BC. a) chứng minh tam giác AMB bằng tam giác AMC. b) từ M kẻ ME vuông góc với AB và MF vuông góc với AC. Chứng minh rằng AE = EF c) chứng minh EF song song với BC b) từ B kẻ đường thẳng vuông góc với AB. Từ C kẻ đường thẳng vuông góc với AC. Hai đường thẳng này cắt nhau tại N. Chứng minh rằng A,M,N thẳng hàng.
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b:Sửa đề: Chứng minh AE=AF
Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
nên EF//BC
d: Xét ΔABN vuông tại B và ΔACN vuông tại C có
AN chung
AB=AC
Do đó: ΔABN=ΔACN
=>BN=CN
=>N nằm trên đường trung trực của BC(1)
Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,M,N thẳng hàng
cho tam giác abc cân tại a gọi h là trung điểm của bc
a, Chứng minh AH vuông góc với BC
b, Kẻ HE vuong góc với AB tại E ; HF vuông góc với AC tại F . Chứng minh HE = HF
c, Chứng minh tam giác AEF là tam giác cân
d, Chứng minh EF song song BC