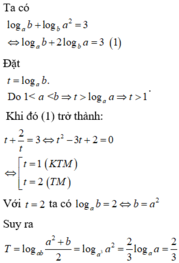Cho a,b là các số hữu tỉ khác 0 thõa mãn đk a/b=ab=a+b tính giá trị của biểu thức T=a2 +b2

Những câu hỏi liên quan
Cho a, b, c là ba số khác 0 thỏa mãn: ab/a+b=bc/b+c=ca/c+a ( với giả thiết các tỉ số đều có nghĩa) và a+b=c=1 tính giá trị của biểu thức A=abc(a2+b2+c2)/ab+bc+ca
\(\dfrac{ab}{a+b}=\dfrac{bc}{b+c}=\dfrac{ca}{c+a}\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{c}+\dfrac{1}{a}\)
\(\Rightarrow\dfrac{1}{a}=\dfrac{1}{b}=\dfrac{1}{c}=\dfrac{1+1+1}{a+b+c}=\dfrac{3}{a+b+c}=\dfrac{3}{1}=3\)
\(\Rightarrow a=b=c=\dfrac{1}{3}\)
\(\Rightarrow A=\dfrac{a^3\left(a^2+b^2+c^2\right)}{a^2+b^2+c^2}=a^3=\left(\dfrac{1}{3}\right)^3=\dfrac{1}{27}\)
Đúng 0
Bình luận (0)
cho a,b là các số hữu tỉ khác 0 thỏa mãn điều kiện a:b=ab=a+b. tính giá trị biểu thức T=a^2+b^2
a : b = ab
=> a = ab.b = ab^2
=> b^2 = 1 ( vì a,b khác 0 )
=> b=+-1
+, Nếu b=-1
Có : ab = a+b
=> -a = a+1
=> a=-1/2
=> T = 5/4
+, Nếu b = 1
Có : ab = a+b
=> a = a+1
=> ko tồn tại a t/m
Vậy T = 5/4
Tk mk nha
Đúng 0
Bình luận (0)
cho a,b là các số hữu tỉ khác 0; thỏa mãn điều kiện : a/b=ab=a+b. Tính giá trị của biểu thức T=a2 + b2
Cho số phức
z
a
+
b
i
(a, b là các số thực) thỏa mãn
z
.
z
+
2
z
+
i
0.
Tính giá trị của biểu thức
T
a
2
+
b
2
.
A.
T...
Đọc tiếp
Cho số phức z = a + b i (a, b là các số thực) thỏa mãn z . z + 2 z + i = 0. Tính giá trị của biểu thức T = a 2 + b 2 .
A. T = 4 3 − 2.
B. T = 3 + 2 2 .
C. T = 3 − 2 2 .
D. T = 4 + 2 3 .
Đáp án C
a 2 + b 2 ( a + b i ) + 2 ( a + b i ) + i = 0 ⇔ a a 2 + b 2 + 2 a + ( b a 2 + b 2 + 2 b + 1 ) i = 0 ⇔ a a 2 + b 2 + 2 a = 0 b a 2 + b 2 + 2 b + 1 = 0 ⇒ a = 0 b = 1 ± 2 ⇒ a = 0 b = 1 − 2 ⇒ T = 1 - 2 2 = 3 − 2 2
Đúng 0
Bình luận (0)
Cho hai số thực a và b thõa mãn a+b= 4ab, a,b<=1. tìm giá trị lớn nhất của biểu thức P= a2+ b2
Cho a,b là các số hữu tỉ khác 0,thỏa mãn điều kiện a/b=a+b.Tính giá trị của biểu thức T=a2+b2
Cho các số thực a, b thỏa mãn 1 a b và
log
a
b
+
log
b
a
2
3
. Tính giá trị của biểu thức
T
log
a
b
a
2
+
b
2
A.
1...
Đọc tiếp
Cho các số thực a, b thỏa mãn 1< a < b và log a b + log b a 2 = 3 . Tính giá trị của biểu thức T = log a b a 2 + b 2
A. 1 6
B. 3 2
C. 6
D. 2 3
Cho a,b,c là ba số khác 0 thõa mãn:\(\frac{ab}{a+b}=\frac{bc}{b+c}=\frac{ca}{c+a}\)(với giả thiết các tỉ số đều có nghĩa). Tính giá trị của biểu thức
M\(\frac{ab+bc+ca}{a^2+b^2+c^2}\)
Câu hỏi của Đậu Đình Kiên - Toán lớp 7 - Học toán với OnlineMath
cho các số a, b, c thỏa mãn a2+b2=c2+d2=2022 và ad+bc=0. Tính giá trị của biểu thức a3b3+c3d3
\(\left(ad+bc\right)\left(a^2d^2+b^2c^2\right)=0\)
\(\Rightarrow a^3d^3+adb^2c^2+bca^2d^2+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd\left(bc+ad\right)+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd.0+b^3c^3=0\)
\(\Rightarrow a^3d^3+b^3c^3=0\)
Đúng 2
Bình luận (2)