Một phân xưởng có hai máy đặc chủng M1, M2 sản xuất hai loại sản phẩm kí hiệu I; II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại I phải dùng máy M1 trong 3h và máy M2 trong 1h. Một máy không thể sản xuất đồng thời hai sản phẩm trreen. Máy M1 làm việc không quá 6h trong một ngày, máy M2 một ngày chỉ làm việc không quá 4h. Kế hoạch sản xuất sao cho tổng số tiền lãi lớn nhát là

Những câu hỏi liên quan
Một phân xưởng có hai máy đặc chủng M1, M2 sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm loại I lãi 6 triệu đồng, một tấn sản phẩm loại II lãi 4,8 triệu đồng. Muốn sản xuất một tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 chỉ làm việc không quá...
Đọc tiếp
Một phân xưởng có hai máy đặc chủng M1, M2 sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm loại I lãi 6 triệu đồng, một tấn sản phẩm loại II lãi 4,8 triệu đồng. Muốn sản xuất một tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 chỉ làm việc không quá 4 giờ. Gỉa sử số tấn sản phẩm loại I, II sản xuất trong một ngày lần lượt là x,y
a) viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó
b) gọi F( triệu đồng ) là số tiền lãi thu được trong một ngày
c) Cần sản xuất bao nhiêu tấn sản phẩm loại I và loại II trong một ngày để số tiền lãi thu được là cao nhất
Bài 3: Một phân xưởng có hai máy đặc chủng M1, M2 sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 một ngày chỉ làm...
Đọc tiếp
Bài 3: Một phân xưởng có hai máy đặc chủng M1, M2 sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 một ngày chỉ làm việc không quá 4 giờ. Hãy đặt kế hoạch sản xuất sao cho tổng số tiền lãi cao nhất.
Một xưởng sản xuất có hai máy đặc chủng A, B sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng máy A trong 6 giờ và dùng máy B trong 2 giờ. Để sản xuất một tấn sản phẩm Y cần dùng máy A trong 2 giờ và dùng máy B trong 2 giờ. Cho biết mỗi máy không thể sản xuất đồng thời hai loại sản phẩm. Máy A làm việc không quá 12 giờ một ngày, máy B làm việc không quá 8 giờ một ngày. Một tấn sản phẩm X lãi 10 triệu đồng và một tấn sản phẩm Y lãi 8 triệu đồng. Hãy lập kế hoạch sản xuất m...
Đọc tiếp
Một xưởng sản xuất có hai máy đặc chủng A, B sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng máy A trong 6 giờ và dùng máy B trong 2 giờ. Để sản xuất một tấn sản phẩm Y cần dùng máy A trong 2 giờ và dùng máy B trong 2 giờ. Cho biết mỗi máy không thể sản xuất đồng thời hai loại sản phẩm. Máy A làm việc không quá 12 giờ một ngày, máy B làm việc không quá 8 giờ một ngày. Một tấn sản phẩm X lãi 10 triệu đồng và một tấn sản phẩm Y lãi 8 triệu đồng. Hãy lập kế hoạch sản xuất mỗi ngày sao cho tổng số tiền lãi cao nhất.
Tham khảo:
Gọi x, y lần lượt là số tấn sản phẩm X, Y mà xưởng cần sản xuất mỗi ngày.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Máy A làm việc không quá 12 giờ một ngày nên \(6x + 2y \le 12\)
- Máy B làm việc không quá 8 giờ một ngày nên \(2x + 2y \le 8\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.
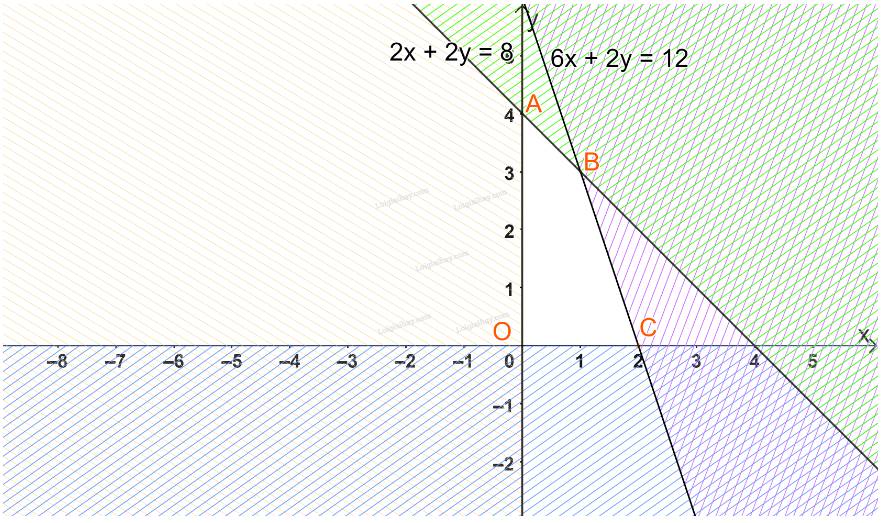
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(0;4),\)\(B(1;3),\)\(C(2;0).\)
Gọi F là số tiền lãi (đơn vị: triệu đồng) thu về, ta có: \(F = 10x + 8y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 10.0 + 8.0 = 0\)
Tại \(A(0;4):\)\(F = 10.0 + 8.4 = 32\)
Tại \(B(1;3),\)\(F = 10.1 + 8.3 = 34\)
Tại \(C(2;0).\)\(F = 10.2 + 8.0 = 20\)
F đạt giá trị lớn nhất bằng \(34\) tại \(B(1;3).\)
Vậy xưởng đó nên sản xuất 1 tấn sản phầm loại X và 3 tấn sản phầm loại Y để tổng số tiền lãi là lớn nhất.
Đúng 0
Bình luận (0)
Một xưởng sản xuất có hai máy, sản xuất ra hai loại sản phẩm I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Để sản xuất một tấn sản phẩm loại I cần máy thứ nhất làm việc trong 3 giờ, máy thứ hai làm việc trong 1 giờ. Để sản xuất một tấn sản phẩm loại II cần máy thứ nhất làm việc trong 1 giờ, máy thứ hai làm việc trong 1 giờ. Một ngày máy thứ nhất làm việc không quá 6 giờ, máy thứ hai làm việc không quá 4 giờ. Hỏi một ngày tiền lãi lớn nhất là bao...
Đọc tiếp
Một xưởng sản xuất có hai máy, sản xuất ra hai loại sản phẩm I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Để sản xuất một tấn sản phẩm loại I cần máy thứ nhất làm việc trong 3 giờ, máy thứ hai làm việc trong 1 giờ. Để sản xuất một tấn sản phẩm loại II cần máy thứ nhất làm việc trong 1 giờ, máy thứ hai làm việc trong 1 giờ. Một ngày máy thứ nhất làm việc không quá 6 giờ, máy thứ hai làm việc không quá 4 giờ. Hỏi một ngày tiền lãi lớn nhất là bao nhiêu?
![]()
![]()
![]()
![]()
Một xí nghiệp sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại Ii lãi 1,6 triệu đồng. Muốn sản xuất 1 tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất 1 tấn sản phẩm loại II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Biết rằng một máy không thể sản xuất đồng thời hai loại sản phẩm; máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 một ngày chỉ làm việc không quá 4 giờ.
Hãy đặt kế hoạ...
Đọc tiếp
Một xí nghiệp sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại Ii lãi 1,6 triệu đồng. Muốn sản xuất 1 tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất 1 tấn sản phẩm loại II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Biết rằng một máy không thể sản xuất đồng thời hai loại sản phẩm; máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 một ngày chỉ làm việc không quá 4 giờ.
Hãy đặt kế hoạch sản xuất của xí nghiệp sao cho tổng số tiền lãi cao nhất.
A) một ngày sản xuất 1 tấn sản phẩm loại I và 3 tấn sản phẩm loại II.
B) một ngày sản xuất 1 tấn sản phẩm loại II và 3 tấn sản phẩm loại I.
C) một ngày sản xuất 2 tấn sản phẩm loại I và 2 tấn sản phẩm loại II.
D) một ngày sản xuất 3 tấn sản phẩm loại II.
Mn giải giúp e câu này vs ạ Một phân xưởng có 3 máy I, II, III cùng sản xuất một loại sản phẩm. Sản phẩm của các máynày sản xuất ra chiếm tỉ lệ lần lượt là 35%; 40%; 25 % toàn bộ sản lượng của phân xưởng. Tỉ lệ phế phẩmcủa các máy này tương ứng là 1%; 1.5%; 0.8%. Lấy ngẫu nhiên một sản phẩm của phân xưởng để kiểm tra:a. Tính xác suất lấy được phế phẩm (H);b. Giả sử sản phẩm lấy ra là phế phẩm. Tính xác suất sản phẩm đó do máy II sản xuất.
Đọc tiếp
Mn giải giúp e câu này vs ạ
Một phân xưởng có 3 máy I, II, III cùng sản xuất một loại sản phẩm. Sản phẩm của các máy
này sản xuất ra chiếm tỉ lệ lần lượt là 35%; 40%; 25 % toàn bộ sản lượng của phân xưởng. Tỉ lệ phế phẩm
của các máy này tương ứng là 1%; 1.5%; 0.8%. Lấy ngẫu nhiên một sản phẩm của phân xưởng để kiểm tra:
a. Tính xác suất lấy được phế phẩm (H);
b. Giả sử sản phẩm lấy ra là phế phẩm. Tính xác suất sản phẩm đó do máy II sản xuất.
Hai phân xưởng cùng sản xuất một loại chi tiết máy.Phân xưởng I làm trong 10 ngày,phân xưởng II làm trong 12 ngày được tất cả 13700 chi tiết máy,mỗi phân xưởng sản xuất được bao nhiêu chi tiết máy.Biết cứ 12 ngày thì số chi tiết máy của phân xưởng I sản xuất hơn phân xưởng II vừa bằng số chi tiết máy phân xưởng II sản xuất trong một ngày
Hai phân xưởng sản xuất được 564 sản phẩm.Nếu phân xưởng thứ nhất sản xuất thêm 69 sản phẩm thì số sản phẩm mà hai phân xưởng sản xuất được bằng nhau. Hỏi mỗi phân xưởng có bao nhiêu sản phẩm
Phân xưởng sản xuất trong quý I được 345 sản phẩm, quý II sản xuất hơn quý I 24 sản phẩm. Quý III, phân xưởng sản xuất số sản phẩm bằng trung bình cộng hai quý đầu. Quý IV, phân xưởng sản xuất được 449 sản phẩm. Trung bình mỗi quý phân xưởng sản xuất được bao nhiêu sản phẩm.
Số sản phẩm phân xưởng đó sản xuất trong quý II là:
\(345+24=369\) (sản phẩm)
Số sản phẩm phân xưởng đó sản xuất trong quý III là:
\(\dfrac{\left(345+369\right)}{2}=357\) (sản phẩm)
Trung bình mỗi quý phân xưởng sản xuất được là:
\(\dfrac{\left(345+369+357+449\right)}{4}=380\) (sản phẩm)
Đúng 1
Bình luận (0)


















