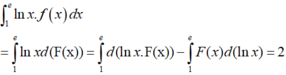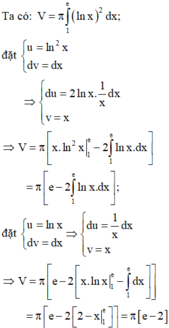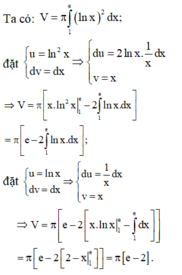Tích phân từ 1 đến e của lnx/x

Những câu hỏi liên quan
Tích phân từ 1 đến e của lnx/x
= 1 / e . ( t/p từ 1->e ( e.lnx / ( x + 1 ) ) dx
= 1 / e . ( tp từ 1->e ( ln(x+1) / ( x + 1 ) ) dx < e.lnx = ln ( x + 1 ) mà >
= 1 / e . ( tp từ 1->e ( ln(x+1) d ( ln ( x + 1 ) )
= 1 / e . ( 1 /2 . ln^2 (( x + 1 )) |1->e )
= ( ln^2 (( e + 1 )) - ln2 ) / 2e
Đúng 0
Bình luận (0)
\(I=\int_1^e\dfrac{\ln x}{x}dx=\int_1^e\ln x.d(\ln x)=\dfrac{(\ln x)^2}{2}|_1^e=...\)
Đúng 0
Bình luận (0)
Đổi biến u=lnx thì tích phân từ 1 đến e của (1-lnx)/x^2 thành
Lời giải:
\(I=\int ^{e}_{1}\frac{1-\ln x}{x^2}dx=\int ^{e}_{1}\frac{dx}{x^2}-\int ^{e}_{1}\frac{\ln x}{x^2}dx\)
Ta có \(\int ^{e}_{1}\frac{dx}{x^2}=\left.\begin{matrix} e\\ 1\end{matrix}\right|\frac{-1}{x}=\frac{-1}{e}+1\)
Đặt \(\left\{\begin{matrix} u=\ln x\\ dv=\frac{dx}{x^2}\end{matrix}\right.\)\(\Rightarrow \left\{\begin{matrix} du=\frac{dx}{x}\\ v=\frac{-1}{x}\end{matrix}\right.\)
\(\Rightarrow \int ^{e}_{1}\frac{\ln xdx}{x^2}=\frac{-\ln x}{x}+\int ^{e}_{1}\frac{dx}{x^2}=\left.\begin{matrix} e\\ 1\end{matrix}\right|\left ( \frac{-\ln x}{x}-\frac{1}{x} \right )=1-\frac{2}{e}\)
Do đó mà \(I=1-\frac{1}{e}-(1-\frac{2}{e})=\frac{1}{e}\)
Đúng 0
Bình luận (0)
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn
∫
1
e
F
(
x
)
d
(
ln
x
)
3
và
F
(
e
)
5
Tích phân
∫
1
e
ln
x
.
f
(
x
)
d
x
bằng
Đọc tiếp
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn ∫ 1 e F ( x ) d ( ln x ) = 3 và F ( e ) = 5 Tích phân ∫ 1 e ln x . f ( x ) d x bằng
![]()
![]()
![]()
![]()
Cho hàm số f(x) thỏa mãn: xf'(x).lnx + f(x) = 2x2, ∀x ∈ (1;+∞) và f(e) = e2. Tính tích phân I=\(\int\limits^{e^2}_e\dfrac{x}{f\left(x\right)}dx\)
Cách làm cơ bản của dạng này:
Cho hàm số y=f(x) liên tục trên R\ {0; -1} thỏa mãn f(1) =-2ln2 và\(x\left(x+1\right)f'\left(x\right)+f\left(x\right)=x^... - Hoc24
Đúng 1
Bình luận (1)
Tính tích phân \(I=\int_1^e\dfrac{xln^2x}{\left(lnx+1\right)^2}dx\)
\(I=\int\limits^e_1x^2.ln^2x.\dfrac{1}{x\left(lnx+1\right)^2}dx\)
Đặt \(\left\{{}\begin{matrix}u=x^2ln^2x\\dv=\dfrac{1}{x\left(lnx+1\right)^2}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2x.lnx\left(lnx+1\right)\\v=-\dfrac{1}{lnx+1}\end{matrix}\right.\)
\(\Rightarrow I=-\dfrac{x^2ln^2x}{lnx+1}|^e_1+\int\limits^e_12x.lnxdx=-\dfrac{e^2}{2}+I_1\)
Xét \(I_1\), đặt \(\left\{{}\begin{matrix}u=lnx\\dv=2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=x^2\end{matrix}\right.\)
\(\Rightarrow I_1=x^2lnx|^e_1-\int\limits^e_1xdx=...\)
Đúng 0
Bình luận (0)
Tích phân từ 1 đến e của ln(x+1)/x
tích phân từ 0 đến 1 ( X^2 + 1 ) x e^xdx
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng
y
lnx
,
y
0
,
x
1
,
x
e
.
A. e - 2 B. e + 2 C.
π
e
+
2
....
Đọc tiếp
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng y = lnx , y = 0 , x = 1 , x = e .
A. e - 2
B. e + 2
C. π e + 2 .
D. π ( e − 2 ) .
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng
y
ln
x
;
y
0
;
x
1
;
x
e
A. e - 2 B. e + 2 C.
π
(
e
+
2
)
D.
π
(
e...
Đọc tiếp
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng y = ln x ; y = 0 ; x = 1 ; x = e
A. e - 2
B. e + 2
C. π ( e + 2 )
D. π ( e - 2 )