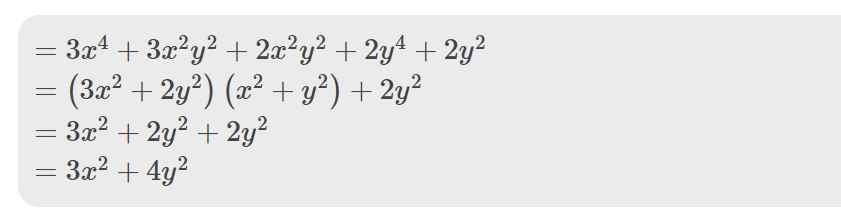Từ \(x^2-2xy+2y^2-2x+6y+5=0\)

\(\Rightarrow\left(x^2-2xy-2x+y^2+2y+1\right)+\left(y^2+4y+4\right)=0\)

\(\Rightarrow\left(x-y-1\right)^2+\left(y+2\right)^2=0\)

\(\Rightarrow\left\{\begin{matrix}\left(x-y-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\)\(\Rightarrow\left\{\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)

Thay vào ta có: \(\frac{3x^2y-1}{4xy}=\frac{3\cdot\left(-1\right)^2\cdot\left(-2\right)-1}{4\cdot\left(-1\right)\cdot\left(-2\right)}=-\frac{7}{8}\)

ai lớp-8 thj lm hộ mk dj,mk đg cần gap

chịu ak

Từ đề bài \(\Rightarrow\left(x^2+2xy+y^2\right)-2x-2y+1+y^2-4y+4=0\)

\(\Leftrightarrow\left(x+y\right)^2-2\left(x+y\right)+1+y^2-4y+4=0\)

\(\Leftrightarrow\left(x+y-1\right)^2+\left(y-2\right)^2=0\)

Lập luận tìm được \(x=-1;y=2\)  thay vào A (tự tính)

Thay x=-2 và y=-1 vào biểu thức \(5x^2y-4xy^2\), ta được:

\(5\cdot\left(-2\right)^2\cdot\left(-1\right)-4\cdot\left(-2\right)\cdot\left(-1\right)^2\)

\(=-5\cdot4+8\cdot1\)

\(=-20+8=-12\)

Vậy: -12 là giá trị của biểu thức \(5x^2y-4xy^2\) tại x=-2 và y=-1

Thay x=-2 và y=-1 vào biểu thức \(5x^2y-4xy^2\) ta được

\(5.\left(-2\right)^2.\left(-1\right)-4.\left(-2\right).\left(-1\right)^2\)

=\(\left(-5\right).4+8.1=-12\)

Vậy giá trị của biểu thức \(5x^2y-4xy^2\) tại x=-2 và y=-1 là -12

Nhớ tick cho mình nha!

\(A=2x^2+4xy-4x+2y^2-10xy+4y+2xy\)

\(A=\left(2x^2-4xy+2y^2\right)-\left(4x-4y\right)=2\left(x^2-2xy+y^2\right)-4\left(x-y\right)\)

\(A=2\left(x-y\right)^2-4\left(x-y\right)=2.3^2-4.3=6\)

\(T=x^2+2xy+2y^2-2x-2y-2\)

\(=\left(x^2+2xy+y^2-2x-2y+1\right)+y^2-3\)

\(=\left(x+y-1\right)^2+y^2-3\ge-3\)

Đẳng thức xảy ra khi \(\begin{cases}\left(x+y-1\right)^2=0\\y^2=0\end{cases}\)\(\Rightarrow\begin{cases}x+y-1=0\\y=0\end{cases}\)

\(\Rightarrow\begin{cases}x+0-1=0\\y=0\end{cases}\)\(\Rightarrow\begin{cases}x=1\\y=0\end{cases}\)

Vậy \(Min_T=-3\) khi \(\begin{cases}x=1\\y=0\end{cases}\)

\(=3x^4+3x^2y^2+2x^2y^2+2y^4+2y^2\)

\(=\left(3x^2+2y^2\right)\left(x^2+y^2\right)+2y^2\)

\(=3x^2+2y^2+2y^2\)

\(=3x^2+4y^2\)