Giúp e vs ạ e cảm ơnn nhiều ạ💦

Những câu hỏi liên quan
Giúp e vs ạ e cảm ơnn
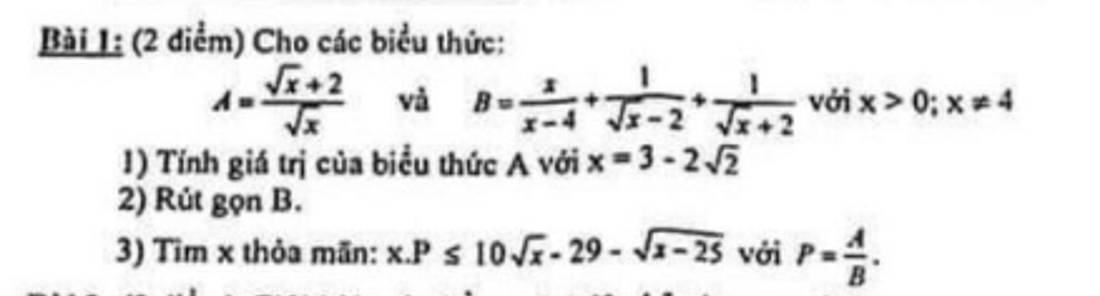
mn giúp e phần c vs ạ
e cảm ơnn
1: Khi x=3-2 căn 2 thì \(A=\dfrac{\sqrt{2}-1+2}{\sqrt{2}-1}=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}=3+2\sqrt{2}\)
2: \(B=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{x-4}=\dfrac{x+2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
3: \(P=A:B=\dfrac{\sqrt{x}+2}{\sqrt{x}}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{x-4}{x}\)
\(x\cdot P< =10\sqrt{x}-29-\sqrt{x-25}\)
=>\(x-4< =10\sqrt{x}-29-\sqrt{x-25}\)
\(\Leftrightarrow x-4-10\sqrt{x}+29< =-\sqrt{x-25}\)
=>\(x-10\sqrt{x}+25< =-\sqrt{x-25}\)
=>(căn x-5)^2<=-căn x-25
=>x-25=0
=>x=25
Đúng 0
Bình luận (1)
Giúp em vs ạ cảm ơnn rất nhiều 
giúp e với ạ e cảm ơnn
Đọc tiếp
giúp e với ạ e cảm ơnn
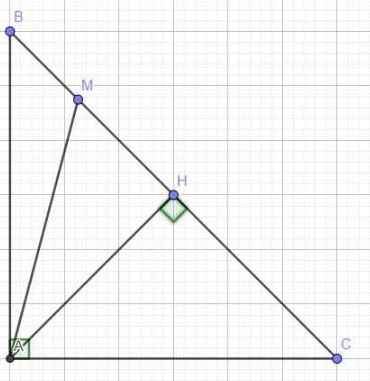
a)Kẻ AH⊥BC
Vì ΔABC vuông cân tại A
⇒ AH cũng là đường trung tuyến
⇒ AH=BH=CH
Ta có:MB2 + MC2 = (BH-HM)2 + (CH+HM)2 = (AH-HM)2+(AH+HM)2
= AH2-2.AH.HM+HM2+AH2+2.AH.HM+HM2=2(AH2+HM2)
Áp dụng định lý Py-ta-go vào ΔAHM vuông tại A ta có:
MA2 = AH2+HM2
⇒ MB2+MC2=2MA2
b) Ta có: MA≥AH (đường xiên và đường vuông góc)
⇒ MA2 ≥ AH2
⇒ 2MA2 ≥ 2AH2
⇒ MB2+MC2 ≥ 2AH2
Dấu "=" xảy ra ⇔ MA=AH ⇔ M là trung điểm của BC
Vậy Min K = 2AH2 ⇔ M là trung điểm của BC
Đúng 1
Bình luận (0)
 làm rõ giúp e ạ, e cảm ơnn
làm rõ giúp e ạ, e cảm ơnn
4:
Vẽ OM vuông góc CD
=>OM vuông góc HK
Xét hình thang AHKB có
O là trung điểm của AB
OM//AH//BK
=>M là trung điểm của HK
=>MH=MK
ΔOCD cân tại O
mà OM là đường cao
nên M là trung điểm của CD
=>MC=MD
MC+CH=MH
MD+DK=MK
mà MH=MK và MC=MD
nên CH=DK
Đúng 1
Bình luận (0)

GIÚP EM VỚI Ạ E CẢM ƠNN
a: Để A là phân số thì \(n+1\ne0\)
=>\(n\ne-1\)
b: \(n^2-1=0\)
=>\(n^2=1\)
=>\(\left[{}\begin{matrix}n=1\left(nhận\right)\\n=-1\left(loại\right)\end{matrix}\right.\)
Thay n=1 vào A, ta được:
\(A=\dfrac{3\cdot1-1}{1+1}=\dfrac{3-1}{2}=1\)
c: Để A là số nguyên thì \(3n-1⋮n+1\)
=>\(3n+3-4⋮n+1\)
=>\(-4⋮n+1\)
=>\(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)
d: \(A=\dfrac{3n-1}{n+1}=\dfrac{3n+3-4}{n+1}=3-\dfrac{4}{n+1}\)
Để A min thì \(\dfrac{-4}{n+1}\) min
=>n+1 là số nguyên dương nhỏ nhất
=>n+1=1
=>n=0
=>\(A=3-\dfrac{4}{0+1}=3-4=-1\)
Đúng 0
Bình luận (0)
345:167= bao nhiêu ạ giúp em với ạ tuần sau e nộp bài rùi nhưng khó phép này ah chj nào giỏi giúp e với ạ e cảm ơnn
2.06586826347
~Hok tốt~
Giải giúp e bài 1,2 với ạ, em cảm ơnn
Mn giải giúp e vs ạ. E cảm mơn nhiều ạ

\(VT=\sqrt{\dfrac{\sqrt{5}}{8\sqrt{5}+3\sqrt{35}}}.\left(3\sqrt{2}+\sqrt{14}\right)\)
\(=\sqrt{\dfrac{\sqrt{5}}{8\sqrt{5}+3\sqrt{5}.\sqrt{7}}}.\left(3\sqrt{2}+\sqrt{2}.\sqrt{7}\right)\)
\(=\sqrt{\dfrac{\sqrt{5}}{\sqrt{5}\left(8+3\sqrt{7}\right)}}.\left[\sqrt{2}\left(3+\sqrt{7}\right)\right]\)
\(=\sqrt{\dfrac{1}{8+3\sqrt{7}}}.\left[\sqrt{2}\left(3+\sqrt{7}\right)\right]\)
\(=\dfrac{\sqrt{2}\left(3+\sqrt{7}\right)}{\sqrt{8+3\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}.\sqrt{2}\left(3+\sqrt{7}\right)}{\sqrt{2}.\sqrt{8+3\sqrt{7}}}\) (Nhân \(\sqrt{2}\) cả tử và mẫu)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\sqrt{16+6\sqrt{7}}}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\sqrt{\left(3+\sqrt{7}\right)^2}}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{\left|3+\sqrt{7}\right|}\)
\(=\dfrac{2\left(3+\sqrt{7}\right)}{3+\sqrt{7}}\)
\(=2=VP\left(dpcm\right)\)
Đúng 4
Bình luận (1)





















