mọi người giúp em bài 2 với ạ 

Những câu hỏi liên quan
 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
Bài 2:
a: \(\text{Δ}=\left(-2\right)^2-4\left(m-3\right)=4-4m+12=-4m+16\)
Để pt vô nghiệm thì -4m+16<0
=>m>4
Để phương trình co nghiệmduy nhất thì -4m+16=0
=>m=4
Để phương trình có hai nghiệm phân biệt thì -4m+16>0
=>m<4
b: \(\text{Δ}=\left(2m-2\right)^2-4\left(m^2-m+1\right)\)
\(=4m^2-8m+4-4m^2+4m-4=-4m\)
Để pt vô nghiệm thì -4m<0
=>m>0
Để phương trình co nghiệmduy nhất thì -4m=0
=>m=0
Để phương trình có hai nghiệm phân biệt thì -4m>0
=>m<0
c: \(\Delta=\left(-m\right)^2-4\cdot1\cdot1=m^2-4\)
Để pt vô nghiệm thì m^2-4<0
=>-2<m<2
Để phương trình co nghiệmduy nhất thì m^2-4=0
=>m=2 hoặc m=-2
Để phương trình có hai nghiệm phân biệt thì m^2-4>0
=>m>2 hoặc m<-2
Đúng 1
Bình luận (0)
Mọi người giúp em với ạ:Em hãy làm 1 bài văn nghị luận về câu tục ngữ"UỐNG NƯỚC NHỚ NGUỒN"khoảng 400 chữ:thứ 2 em thi rồi mọi người giúp em với ạ mọi người hạn chế dùng văn mẫu ạ em chân thành cảm ơn.
Giúp em 2 bài này với ạ, dạ em ghi nhầm x thành n ạ mọi người giúp với bỏ qua cho em
3) \(\sqrt{\left(x-2\right)\left(x+1\right)}\) thì (x-2)(x+1)>0
=> x2 -x-2>0
=> x2 - x - \(\dfrac{1}{2}\)- \(\dfrac{3}{2}\)>0
= (x+\(\dfrac{1}{4}\))2 - 3/2 >0
=> x+ 1/4>3/2
=> x>5/4
4) Có x đâu mà tìm bạn??
Đúng 1
Bình luận (9)
4) \(\sqrt{x^2+2x+1}\) + \(\sqrt{x^2-2x+1}\)= \(\sqrt{\left(x+1\right)^2}\) + \(\sqrt{\left(x-1\right)^2}\)
=> /x+1/+/x-1/ = 2
=> /2x/ = 2
=> 2x=2
=> x=1
Đúng 0
Bình luận (0)
Để biểu thức có nghĩa thì (x-2)(x+1)>0
\(\Leftrightarrow\left[{}\begin{matrix}x>2\\x< -1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Mọi người giúp em bài này với ạ!!! Em cảm ơn mọi người nhiều ạ

Câu 10:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\notin\left\{2;-1\right\}\\y\ne-5\end{matrix}\right.\)
\(A=\dfrac{y+5}{x^2-4x+4}\cdot\dfrac{x^2-4}{x+1}\cdot\dfrac{x-2}{y+5}\)
\(=\dfrac{y+5}{y+5}\cdot\dfrac{\left(x^2-4\right)}{x^2-4x+4}\cdot\dfrac{x-2}{x+1}\)
\(=\dfrac{\left(x^2-4\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x^2-4x+4\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x-2\right)^2}=\dfrac{x+2}{x+1}\)
b: \(A=\dfrac{x+2}{x+1}\)
=>A không phụ thuộc vào biến y
Khi x=1/2 thì \(A=\left(\dfrac{1}{2}+2\right):\left(\dfrac{1}{2}+1\right)=\dfrac{5}{2}:\dfrac{3}{2}=\dfrac{5}{2}\cdot\dfrac{2}{3}=\dfrac{5}{3}\)
Câu 12:
a: \(A=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{x^2-9}\)
\(=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x\left(x-3\right)+2x\left(x+3\right)+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-3x+2x^2+6x+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{3x+9}{\left(x+3\right)\left(x-3\right)}=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3}{x-3}\)
b: Khi x=1 thì \(A=\dfrac{3}{1-3}=\dfrac{3}{-2}=-\dfrac{3}{2}\)
\(x+\dfrac{1}{3}=\dfrac{10}{3}\)
=>\(x=\dfrac{10}{3}-\dfrac{1}{3}\)
=>\(x=\dfrac{9}{3}=3\left(loại\right)\)
Vậy: Khi x=3 thì A không có giá trị
c: \(B=A\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x-3}\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x^2-4x+5}\)
\(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(B=\dfrac{3}{x^2-4x+5}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x-2=0
=>x=2
Đúng 1
Bình luận (0)
Mọi người giúp em bài 2 và bài 3 với ạ
Mọi người giúp em câu 1 với mở bài câu 2 với ạ. Em cảm ơn trước ạ!

Mọi người giúp em bài 2 với bài 3 đc ko ạ
Bài 2:
a,gọi các góc a,b,c,d của tứ giác abcd lần lượt là a,b,c,d(a,b,c,d thuộc n,a,b,c,d<360)
=>a/1=b/2=c/3=d/4
Ta có Góc a+b+c+d=360(tổng các góc của 1 tứ giác)=>áp dung tính chất dãy tỉ số bằng nhau ta có a/1=b/2=c/3=d/4=>a+b+c+d/1+2+3+4=360/10=36
=>a=36,b=72,c=108,d=144
b,
b, Có ˆAA^+ˆDD^=36o36o+144o144o
=180o180o
mà 2 góc này ở vị trí slt
=>AB//CD
Đúng 0
Bình luận (0)

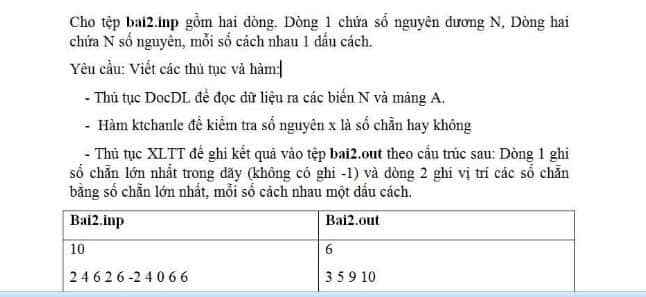
mọi người giúp em 2 bài này với ạ
Bài 2:
#include <bits/stdc++.h>
using namespace std;
long long n,i,a[1000],x;
int main()
{
freopen("bai2.inp","r",stdin);
freopen("bai2.out","w",stdout);
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
for (i=1; i<=n; i++)
if (a[i]%2==0)
{
x=a[i];
break;
}
cout<<x<<endl;
for (i=1; i<=n; i++)
if (a[i]==x) cout<<i<<" ";
return 0;
}
Đúng 0
Bình luận (0)
Dạ mọi người giúp em bài 2 với ạ















