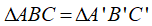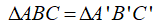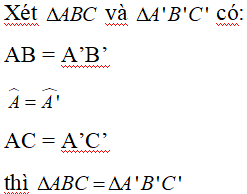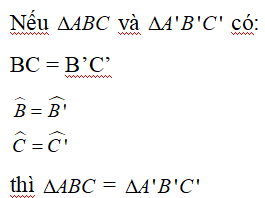Giúp mình với. Cảm ơn mn rất nhiều.

Những câu hỏi liên quan
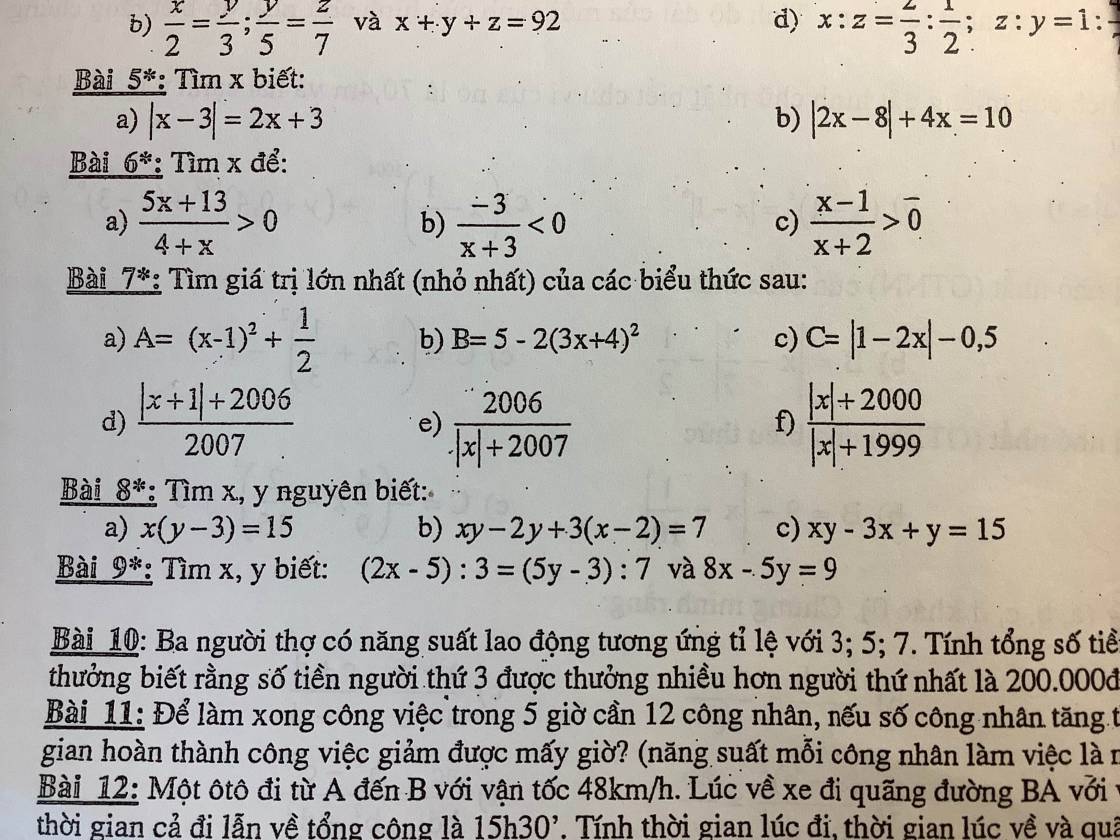
mn giúp mình bài 8 với ạ mình đang cần gấp cảm ơn mn rất nhiều
Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
Đúng 1
Bình luận (0)
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)
Đúng 2
Bình luận (0)
Câu 8:
c.
$xy-3x+y=15$
$\Rightarrow x(y-3)+(y-3)=12$
$\Rightarrow (x+1)(y-3)=12$
Do $x,y$ nguyên nên $x+1, y-3$ nguyên. Mà $(x+1)(y-3)=12$ nên ta xét các TH sau:
TH1: $x+1=1, y-3=12\Rightarrow x=0; y=15$ (tm)
TH2: $x+1=-1; y-3=-12\Rightarrow x=-2; y=-9$ (tm)
TH3: $x+1=12; y-3=1\Rightarrow x=11; y=4$ (tm)
TH4: $x+1=-12; y-3=-1\Rightarrow x=-13; y=2$ (tm)
TH5: $x+1=2; y-3=6\Rightarrow x=1; y=9$ (tm)
TH6: $x+1=-2; y-3=-6\Rightarrow x=-3; y=-3$ (tm)
TH7: $x+1=6; y-3=2\Rightarrow x=5; y=5$ (tm)
TH8: $x+1=-6; y-3=-2\Rightarrow x=-7; y=1$ (tm)
TH9: $x+1=3; y-3=4\Rightarrow x=2; y=7$ (tm)
TH10: $x+1=-3; y-3=-4\Rightarrow x=-4; y=-1$ (tm)
TH11: $x+1=4, y-3=3\Rightarrow x=3; y=6$ (tm)
TH12: $x+1=-4; y-3=-3\Rightarrow x=-5; y=0$ (tm)
Đúng 0
Bình luận (0)
Mn ơi giúp mình với ạ, mik cảm ơn rất nhiều luôn ạ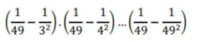
\(=\left(\dfrac{1}{49}-\dfrac{1}{9}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49^2}\right)=0\)
Đúng 1
Bình luận (0)

Mn làm giúp mình bài 8 với ạ mình đang cần gấp cảm ơn mn rất nhiều( giải thích chi tiết ạ).
Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)
Đúng 0
Bình luận (0)
Giúp mình nhanh với ạ mình đang cần rất gấp ạ cảm ơn mn nhiều ạ
giúp gif đề đâu
Xem thêm câu trả lời
Mn giúp mình bài 2,3 nha. Mình cảm ơn rất nhiều 
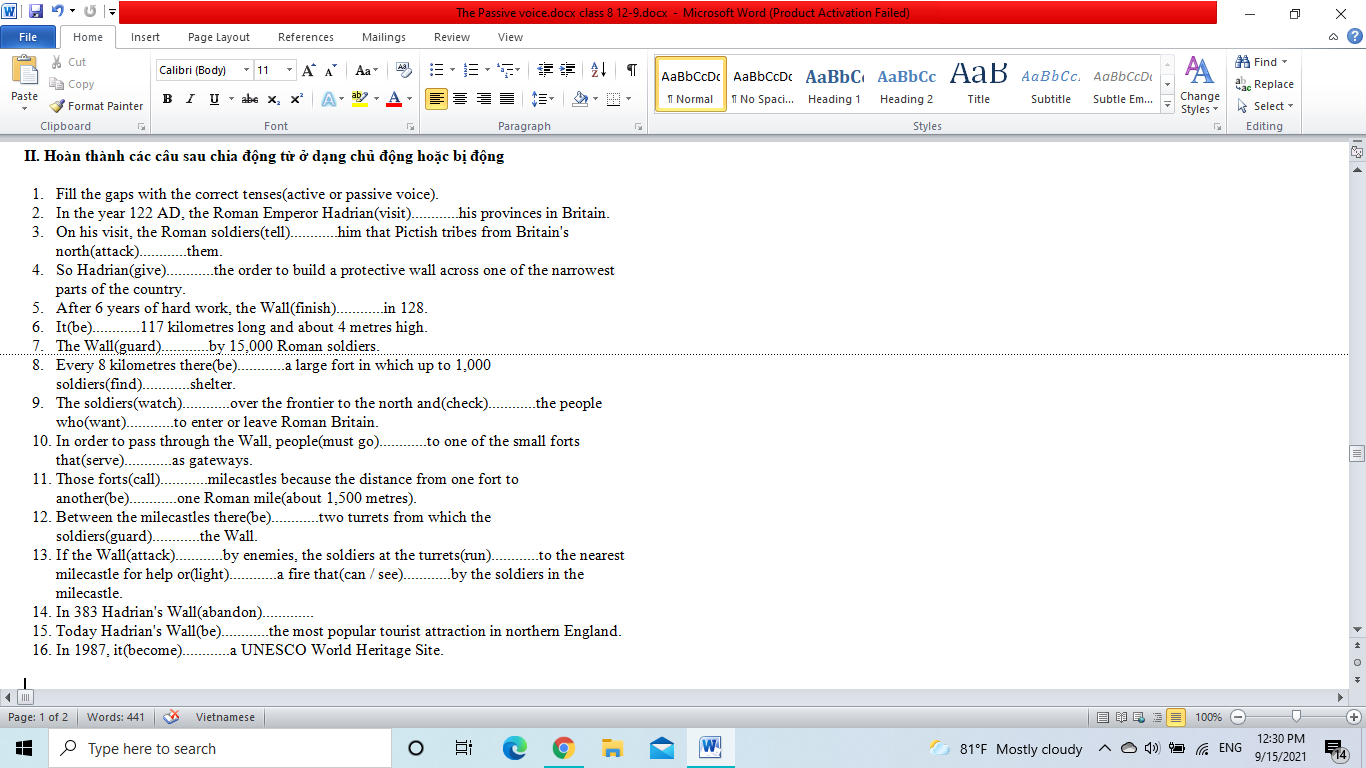
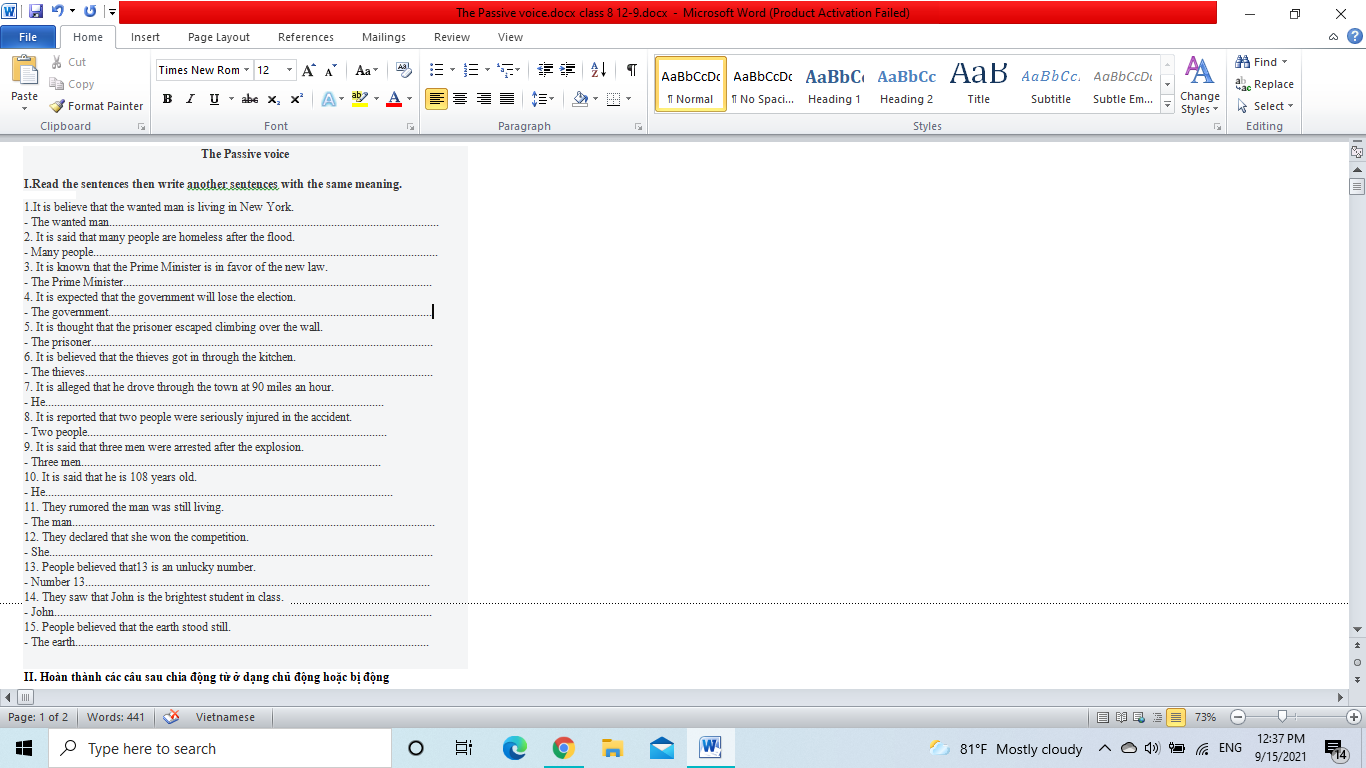 mn ơi giải giúp mk 2 bài này với chiều tầm 3h mình quay lại lấy bài nhé cảm ơn mn rất nhiều.
mn ơi giải giúp mk 2 bài này với chiều tầm 3h mình quay lại lấy bài nhé cảm ơn mn rất nhiều.
giúp mk giải gấp 2 bài này với chiều tầm 3h mình qua lấy nha.cảm ơn mọi người nhiều ah.
Đúng 0
Bình luận (0)
Mn giúp mình câu này nha !! Mình cảm ơn rất nhiều !!!😀😀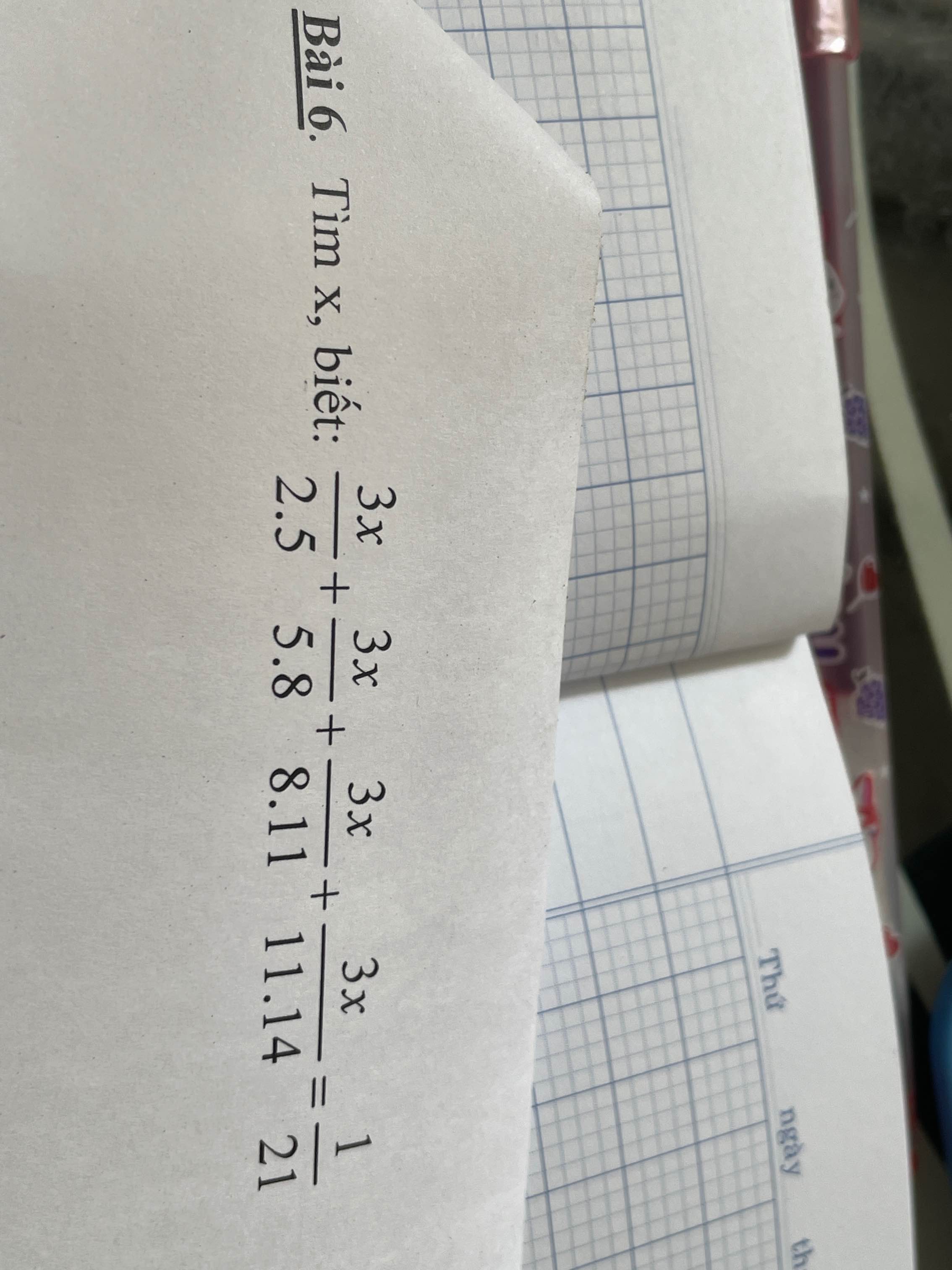
\(\Leftrightarrow x\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}\right)=\dfrac{1}{21}\)
\(\Leftrightarrow x\cdot\dfrac{2}{7}=\dfrac{1}{21}\)
hay \(x=\dfrac{1}{21}:\dfrac{2}{7}=\dfrac{1}{6}\)
Đúng 4
Bình luận (1)
mn giúp mik với,mk đang cần rất gấp ạ! Cảm ơn mn rất nhiều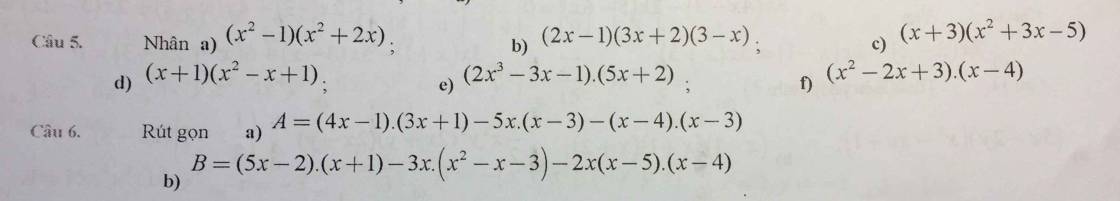
Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2
Đúng 0
Bình luận (0)
Mọi người làm giúp mình bài 1,2 nha. Mình cảm ơn mn người rất nhiều
1. Định nghĩa hai tam giác bằng nhau
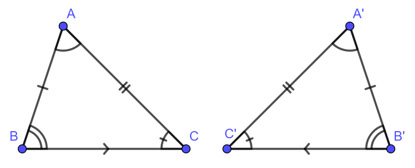
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác vuông
• Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )
• Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )
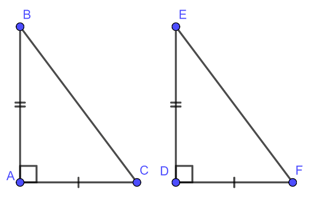
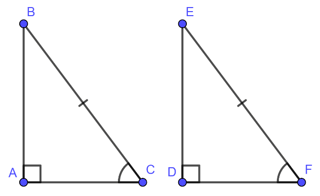
• Cạnh huyền – góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)
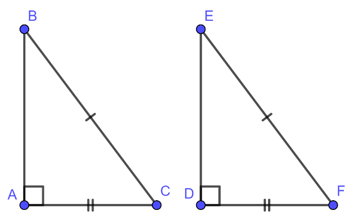
• Cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
1. Định nghĩa hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :
2. Các trường hợp bằng nhau của tam giác
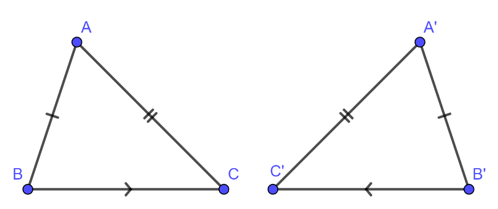
a. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Xét 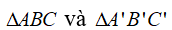
AB = A’B’
AC = A’C’
BC = B’C’
thì
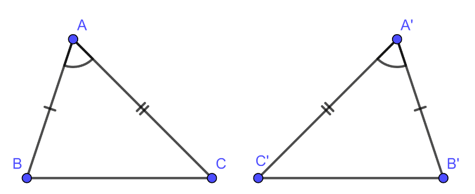
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau
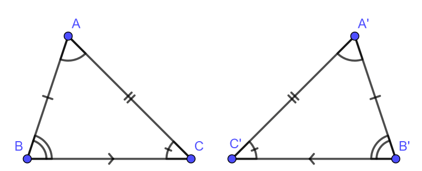
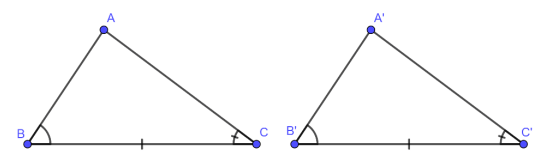
c. Trường hợp bằng nhau thứ ba của hai tam giác: góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
tik cho mình nha mình đc câu1 nè
Đúng 1
Bình luận (0)