1654 x 1763=?
Mn giúp em giải bài này với ạ em cần gấp
 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
3.15:
EF vuông góc MH
NP vuông góc MH
Do đó: EF//NP
3.17:
góc yKH+góc H=180 độ
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ky//Hx
giúp em mấy bài này với mn,em đang cần gấp lắm ạ 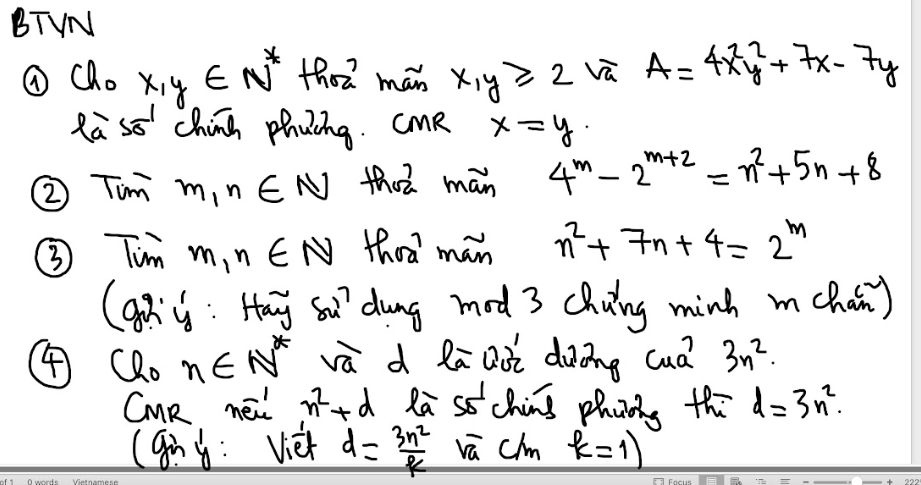
- Đây có phải là toán lớp 8 nữa không vậy :)? Mình học toán nâng cao nhưng chưa bao giờ thấy dạng này :).
b1:
do x;y thuộc số nguyên N và x,y\(\ge\)2
=>\(-4xy+1< +7x-7y< 4xy+1\)
\(\Rightarrow4x^2y^2-4xy+1< 4x^2y^2+7x-7y< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< 4x^2y^2+7x-7y< \left(2xy+1\right)^2\)
mà \(4x^2y^2+7x-7y\) là số chính phương và 1<2xy-1<2xy-1 nên ta có:
\(4x^2y^2+7x-7y-\left(2xy\right)^2\Leftrightarrow x=y\)
1.
TH1: \(x>0\Rightarrow7\left(x-y\right)>0\Rightarrow A>4x^2y^2\)
\(4xy-7x+7y+1>4xy-8x+7y+1=4x\left(y-2\right)+7y+1>0\) do \(x;y\ge2\)
\(\Rightarrow4xy+1>7x-7y\Rightarrow A< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy\right)^2< A< \left(2xy+1\right)^2\)
\(\Rightarrow A\) nằm giữa 2 SCP liên tiếp nên ko thể là SCP
TH2: \(x< y\) , tương tự ta có: \(7\left(x-y\right)< 0\Rightarrow A< 4x^2y^2\)
\(4xy+7x-7y-1>4xy+7x-8y-1=4y\left(x-2\right)+\left(7x-1\right)>0\)
\(\Rightarrow7x-7y>-4xy+1\Rightarrow A>4x^2y^2-4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< A< \left(2xy\right)^2\)
\(\Rightarrow A\) ko thể là SCP
TH3: \(x=y\Rightarrow A=\left(2xy\right)^2\) là SCP (thỏa mãn)
Vậy \(x=y\)
Giúp em giải bài này với ạ em cần gấp lắm ạ
Mn giúp em bài này với ạ chỉ là sắp xếp từ lại thành một cậu thôi bài 29 với 30 mn không cần làm đâu ạ mong cao nhân nào giúp đỡ chứ em đang cần gấp lắm ạ ![]()

what is her mother going to prepare for her bỉthdat party
there are three sticks of butter in the cupboard
i have enough food for the first three day of your stay
 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
chỉ em với :(
3.14:
Ta thấy $\widehat{xNM}=\widehat{xQP}=45^0$. Mà 2 góc này ở vị trí đồng vị nên $MN\parallel PQ$
3.15
$EF\parallel NP$ do cùng vuông góc với $MH$
3.16: Bạn tự vẽ hình nhé.
3.17:
Ta thấy $\widehat{yKH}+\widehat{KHx}=130^0+50^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $Ky\parallel Hx$
Giúp em giải 2 bài này với ạ :< em đnag cần gấp ạ 
 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ
a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)
giúp em bài này với ạ em đang cần giải gấp



Giúp em giải bài này với!!! Em đang cần gấp ạ!!!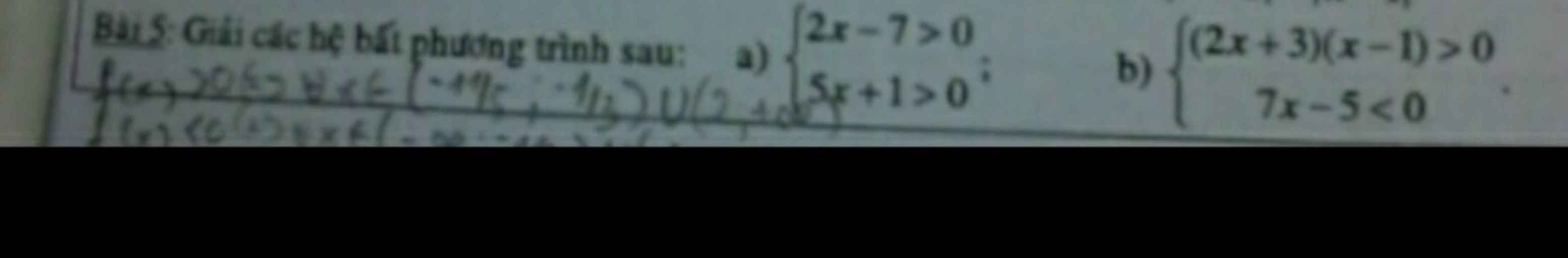
a) \(\left\{{}\begin{matrix}2x-7>0.\\5x+1>0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x>7.\\5x>-1.\end{matrix}\right.\) \(\left\{{}\begin{matrix}x>\dfrac{7}{2}.\\x>\dfrac{-1}{5}.\end{matrix}\right.\)
\(\Rightarrow x>\dfrac{7}{2}.\) \(\Rightarrow x\in\left(\dfrac{7}{2};+\infty\right).\)
Kết luận: Tập nghiệm của hệ bất phương trình trên là \(x\in\left(\dfrac{7}{2};+\infty\right).\)
b) \(\left\{{}\begin{matrix}\left(2x+3\right)\left(x-1\right)>0.\\7x-5< 0.\end{matrix}\right.\) \(\Leftrightarrow\text{}\text{}\)\(\left\{{}\begin{matrix}\left(2x+3\right)\left(x-1\right)>0.\left(1\right)\\x< \dfrac{5}{7}.\left(2\right)\end{matrix}\right.\)
Xét (1):
\(2x+3=0.\Leftrightarrow x=\dfrac{-3}{2}.\\ x-1=0.\Leftrightarrow x=1.\)
Bảng xét dấu:
\(x\) \(-\infty\) \(\dfrac{-3}{2}\) \(1\) \(+\infty\)
\(2x+3\) - \(0\) + | +
\(x-1\) - | - \(0\) +
\(\left(2x+3\right)\left(x-1\right)\) + \(0\) - \(0\) +
Vậy \(\left(2x+3\right)\left(x-1\right)>0.\Leftrightarrow\dfrac{-3}{2}< x< 1.\)
Kết hợp với (2).
\(\Rightarrow\) \(\dfrac{-3}{2}< x< \dfrac{5}{7}.\)
\(\Rightarrow x\in\left(\dfrac{-3}{2};\dfrac{5}{7}\right).\)
Kết luận: Tập nghiệm của hệ bất phương trình trên là \(x\in\left(\dfrac{-3}{2};\dfrac{5}{7}\right).\)