1: Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot\left(m+2\right)\left(3-m\right)\)

\(=\left(2m-2\right)^2+4\left(m+2\right)\left(m-3\right)\)

\(=4m^2-8m+4+4\left(m^2-3m+2m-6\right)\)

\(=4m^2-8m+4+4m^2-4m-24\)

\(=-12m-20\)

Để phương trình có hai nghiệm phân biệt thì Δ>0

\(\Leftrightarrow-12m-20>0\)

\(\Leftrightarrow-12m>20\)

hay \(m< \dfrac{-5}{3}\)

Để phương trình có nghiệm kép thì Δ=0

\(\Leftrightarrow-12m-20=0\)

\(\Leftrightarrow-12m=20\)

hay \(m=\dfrac{-5}{3}\)

Để phương trình vô nghiệm thì Δ<0

\(\Leftrightarrow-12m-20< 0\)

\(\Leftrightarrow-12m< 20\)

hay \(m>\dfrac{-5}{3}\)

2: ĐKXĐ: \(m\ne-2\)

Áp dụng hệ thức Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+2}=\dfrac{2m-2}{m+2}\\x_1\cdot x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)

Ta có: \(x_1+x_2=x_1x_2\)

\(\Leftrightarrow\dfrac{2m-2}{m+2}=\dfrac{3-m}{m+2}\)

Suy ra: 2m-2=3-m

\(\Leftrightarrow2m+m=3+2\)

\(\Leftrightarrow3m=5\)

hay \(m=\dfrac{5}{3}\)(thỏa ĐK)

Xét m=1 phương trình trở thành \(-4x+1=0\)có nghiệm duy nhất x=-1/4

với m#1 ta có \(\Delta'=\left(m+1\right)^2-m\left(m-1\right)=3m+1\)

với \(\hept{\begin{cases}m\ne1\\m>-\frac{1}{3}\end{cases}}\) pt có hai nghiệm phân biệt

với \(m=-\frac{1}{3}\) pt có nghiệm duy nhất

với \(m< -\frac{1}{3}\)pt vô nghiệm,

theo viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{2\left(m+1\right)}{m-1}=2+\frac{4}{m-1}\\x_1x_2=\frac{m}{m-1}=1+\frac{1}{m-1}\end{cases}}\) lấy phương trình trên trừ đi 4 lần phương trình dưới ta có 

\(x_1+x_2-4x_1x_2=-2\)

ý sau, ta có \(\left|x_1-x_2\right|=\frac{2\sqrt{\Delta'}}{\left|a\right|}=\frac{2\sqrt{3m+1}}{\left|m-1\right|}>2\)

\(\frac{\Leftrightarrow4\left(3m+1\right)}{\left(m-1\right)^2}\ge4\Leftrightarrow m^2-5m\le0\Rightarrow m\in\left[0,5\right]\)

kết hợp với đk có 2 nghiệm phân biệt ở câu a , ta có \(m\in\left[0,5\right]\backslash\left\{1\right\}\)

uses crt; 
var a, b: logint; 
Begin 
write('nhap so a ='); Readln(a); 
write('nhap so b ='); readln(b); 
If (a = 0 and b = 0) 
then write ('pt co nghiem x thuoc R') 
else 

(C++) 

#include <bits/stdc++.h>
using namespace std;
int main() {
int a, b;
double x;
cin >> a >> b;
cout << a << "x+" << b << "=0";
cout << "\n<=> x=" << (double)-b/a << endl;
return 0;
}

Chúc bn học tốt!

Bài đầy đủ hơn của mk (bn có thể tham khảo):

#include <bits/stdc++.h>
using namespace std;
int main() {
int a, b;
double x;
cin >> a >> b;
if(a==0) {
    {if(b!=0)
    cout << "Phuong trinh vo nghiem" << "\n";}
    {if(b==0)
    cout << "Phuong trinh co vo so nghiem" << "\n";} }
if (a!=0) {
{ if(b!=0)
   {cout << a << "x+" << b << "=0";
cout << "\n<=> x=" << (double)-b/a << "\n";} }
{
    if(b==0) {
    {
        cout << "x=0" << endl;}
    }
}
}
return 0;
}

Chúc bn học tốt!

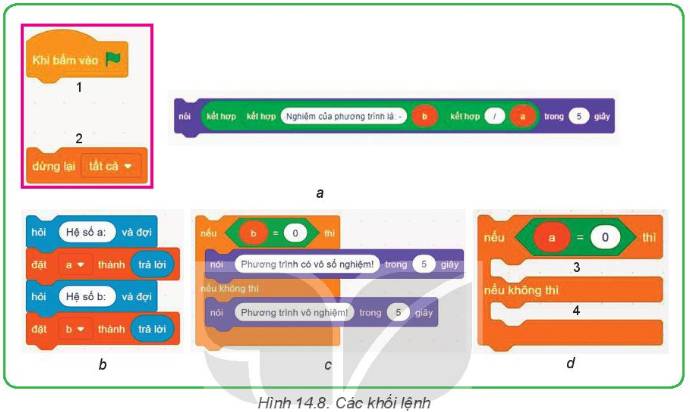
Tham khảo:

Thuật toán giải phương trình ax + b = 0

- Bằng liệt kê tuần tự

Bước 1: Nhập hai số thực a, b

Bước 2. Nếu a = 0

Bước 2.1. Nếu b ≠0 thì thông báo phương trình vô định, rồi kết thúc;

Bước 2.2. Nếu b = 0 thì gán x

Bước 3:  x

Bước 4. Đưa ra nghiệm x, rồi kết thúc.

- Sơ đồ khối:

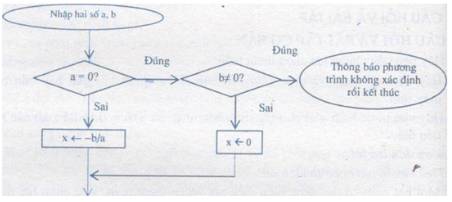
Đề xuất các test tiêu chuẩn

Để xét tất cả các trường hợp có thể xảy ra, ta sử dụng ba bộ test như sau:

i) a = 0, b = 1 (kiểm tra trường hợp phương trình vô định);

ii) a = 0,b = 0 (kiểm tra trường hợp nghiệm x=0);

iii) a = 3, b = 6 (kiểm tra trường hợp nghiêm , y = -b/a).

Pt <=> 1 - x - 2mx = 0

<=> x(2m + 1) = 1

m = -1/2 --> vô nghiệm

m # -1/2 --> x = \(\dfrac{1}{2m+1}\)

1) Với m= 2 PT trở thành  x 2 − 4 x + 3 = 0  

Giải phương trình tìm được các nghiệm  x = 1 ;   x = 3.  

2) Ta có  Δ ' = m 2 − m 2 + 1 = 1 > 0 , ∀ m .  

Do đó, phương trình (1) luôn có hai nghiệm phân biệt.

Từ giả thiết ta có x i 2 − 2 m x i + m 2 − 1 = 0 , i = 1 ; 2. x i 3 − 2 m x i 2 + m 2 x i − 2 = x i x i 2 − 2 m x i + m 2 − 1 + x i − 2 = x i − 2 , i = 1 ; 2.  

Áp dụng định lí Viét cho phương trình (1) ta có  x 1 + x 2 = 2 m ; x 1 . x 2 = m 2 − 1  

Ta có

  x 1 − 2 + x 2 − 2 = 2 m − 4 ; x 1 − 2 x 2 − 2 = x 1 x 2 − 2 x 1 + x 2 + 4 = m 2 − 1 − 4 m + 4 = m 2 − 4 m + 3

Vậy phương trình bậc hai nhận  x 1 3 − 2 m x 1 2 + m 2 x 1 − 2 ,   x 2 3 − 2 m x 2 2 + m 2 x 2 − 2  là nghiệm là x 2 − 2 m − 4 x + m 2 − 4 m + 3 = 0.

Mình cần gấp lắm ạ, ai giúp mình với T-T

2:

#include <bits/stdc++.h>

using namespace std;

long long a[1000],i,n;

int main()

{

cin>>n;

for (i=1; i<=n; i++) cin>>a[i];

for (i=1; i<=n; i++) if (a[i]%2==0) cout<<a[i]<<" ";

return 0;

}

\(mx-x-m+2=0\)

\(x\left(m-1\right)=m-2\)

Nếu m=1 ⇒ \(0x=-1\) (vô nghiệm)

Nếu m≠1 ⇒ \(x=\dfrac{m-2}{m-1}\)

Vậy ...