Xét tam giác ABCABC có phân giác AN=BPAN=BP. Kẻ MN∥AB,PQ∥ABMN∥AB,PQ∥AB. Ta sẽ chứng minh PQ≡MNPQ≡MN
Thật vậy, dễ dàng chứng minh AM=MN,PQ=QBAM=MN,PQ=QB
Xét 2 tam giác cân AMNAMN và PQBPQB có cạnh đáy bằng nhau mà MN>PQMN>PQ (ko mất tính tq, giả sử MNMN gần ABAB hơn PQPQ)
⇒∠PQB>∠NMA⇒∠PQB>∠NMA
⇒∠MAB<∠NBA⇒∠MAB<∠NBA
⇒AM<BN⇒AM<BN
Mà ta lại có AM=MN>PQ=QB>BNAM=MN>PQ=QB>BN (vô lý)
⇒MN≡PQ⇒MN≡PQ

còn lai tu lam nhé!

Xét tam giác DCB và tam giác EBC có :

BC là cạnh chung

Góc CDB = góc CEB = 90 độ

BD = CE

\(\Rightarrow\) tam giác DCB = tam giác ECB (cạnh huyền góc nhọn)

\(\Rightarrow\) Góc DCB = góc EBC hay góc ACB = góc ABC

\(\Rightarrow\) Tam giác ABC cân

Do O thuộc trung tuyến CD của tam giác ABC nên OC = 2/3 CD và OD = 1/3 CD

Do O thuộc trung tuyến BE của tam giác ABC nên OB = 2/3 BE và OE = 1/3 BE

Do CD = BE(theo đề ra) => 2/3 CD = 2/3 BE và 1/3 CD = 1/3 BE<=> OC = OB và OD = OE 

Từ OC = OB => Tam giác BOC cân tại O => Góc OBC = Góc OCB     (1)

Xét tam giác DOB và tam giác EOC có:  OC = OB (chứng minh trên); Góc DOB = Góc EOC(đối đỉnh) ;  OD = OE (chứng minh trên)

=> Tam giác DOB = Tam giác EOC(c.g.c) => Góc OBD = Góc OCE(2 góc tương ứng)         (2)

Cộng từng vế của (1) và (2) ta được : Góc OBC + Góc OBD = Góc OCB + Góc OCE =>Góc DBC = Góc ECB

Mà A;D;B thẳng hàng và A;E;C thẳng hàng =>Góc ABC = Góc ACB =>Tam giác ABC cân tại A

Vậy nếu 1 tam giác có 2 đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.

a,C/m \(\Delta\) MNH la tam giác cân

Xét \(\Delta MNP\) :

MH là đường cao đồng thời là đường trung trực

=> \(\Delta MNP\) cân tại M

b, C/m MH là tia phân giác

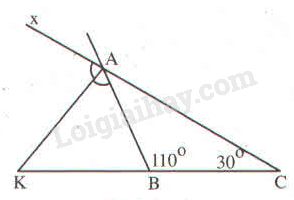
Ta có \(\widehat{xAB}\) là góc ngoài tại đỉnh A của \(\Delta ABC.\)

\(\Rightarrow\widehat{xAB}=\widehat{ABC}+\widehat{ACB}\) (tính chất góc ngoài tam giác).

\(\Rightarrow\widehat{xAB}=110^0+30^0\)

\(\Rightarrow\widehat{xAB}=140^0.\)

Vì \(AK\) là tia phân giác của \(\widehat{BAx}\left(gt\right)\)

\(\Rightarrow\widehat{xAK}=\widehat{KAB}=\frac{\widehat{BAx}}{2}=\frac{140^0}{2}=70^0\) (1)

Lại có: \(\widehat{ABC}+\widehat{ABK}=180^0\) (vì 2 góc kề bù)

\(\Rightarrow110^0+\widehat{ABK}=180^0\)

\(\Rightarrow\widehat{ABK}=180^0-110^0\)

\(\Rightarrow\widehat{ABK}=70^0\) (2)

Từ (1) và (2) \(\Rightarrow\widehat{KAB}=\widehat{ABK}=70^0.\)

Mà 2 góc này thuộc \(\Delta KAB\)

\(\Rightarrow\Delta KAB\) có 2 góc bằng nhau (đpcm).

Chúc bạn học tốt!

a) có AB// DC (gt)

mà E thuộc DC => AB // CE

=> \(\widehat{ABC}=\widehat{ECB}\)

có AC // BE (gt)

=>\(\widehat{ACB}=\widehat{EBC}\)

xét \(\Delta ABC\) và \(\Delta ECB\)

có BC là cạnh chung

\(\widehat{ABC}=\widehat{ECB}\) (cmt)

\(\widehat{ACB}=\widehat{EBC}\) (cmt)

=> \(\Delta ABC=\Delta ECB\) (gcg)

=>BE = CA ( 2 cạnh tương ứng )

b) có AC = BD ( gt)

mà BE = CA (cmt)

=> BD = BE ( = CA)

=>\(\Delta BDE\) là tam giác cân tại B