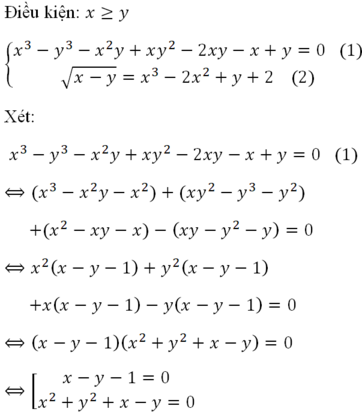tìm nghiệm nguyên của phương trình : x3 - x2y + 3x -2y - 5 = 0

Những câu hỏi liên quan
tìm nghiệm nguyên của phương trình
\(x^2-x^2y+3x-2y-5=0\)
Thiên bình có 102 thứ (1) lớp 8 chưa biết delta
<=> \(\left(x^2+2\right)y=x^2+3x-5\\ \)
\(\Leftrightarrow y=\frac{x^2+3x-5}{x^2+2}=1+\frac{3x-7}{x^2+2}\)
\(y\in Z\Leftrightarrow\frac{3x-7}{x^2+2}\in Z\) \(\Leftrightarrow\left|3x-7\right|\ge x^2+2\)=> \(-4\le x\le1\)
vô nghiệm
Đúng 0
Bình luận (0)
<>x^2(x-y)+2(x-y)+x-5=0(1*)
Denta theox
1-4(x-y)[2(x-y)-5]>=0
<>-8(x-y)^2+20(x-y)+1>=0
<>[-10+V(108)]/-8=<(x-y)=<
[10+V(108)]/8
Vì x-y nguyên nên =>
0=<(x-y)=<2
Vậy để ptr có no nguyên
điều kiện cần là
x-y=0 or x-y=1,x-y=2
Đk đủ:bạn thay lần lượt
các giá trị của x-y ở trên vào 1*
nếu tìm đc x nguyên thì kết luận!
Chúc bạn học tốt
(V(108) là cb2 của 108)
Đúng 0
Bình luận (0)
Tìm tất cả nghiệm nguyên của phương trình 3x – 2y 5 A.
x
5
−
2
t
y
−
5
−
3
t
t...
Đọc tiếp
Tìm tất cả nghiệm nguyên của phương trình 3x – 2y = 5
A. x = 5 − 2 t y = − 5 − 3 t t ∈ ℤ
B. x = 5 + 2 t y = 5 − 3 t t ∈ ℤ
C. x = 5 − 2 t y = 5 + 3 t t ∈ ℤ
D. x = 5 + 2 t y = 5 + 3 t t ∈ ℤ
Ta có 3x – 2y = 5 ⇒ y = 3 x − 5 2 = 2 x + x − 5 2 = 2 x 2 + x − 5 2 = x + x − 5 2
Hay y = x + x − 5 2
Đặt x − 5 2 = t t ∈ ℤ ⇒ x = 2t + 5
⇒ y = 2t + 5 + t ⇔ y = 3t + 5 ⇒ x = 5 + 2 t y = 5 + 3 t t ∈ ℤ
Đáp án: D
Đúng 0
Bình luận (0)
tìm nghiệm nguyên của phương trình 3x-2y=5 ?
http://pitago.vn/question/tim-nghiem-nguyen-cua-phuong-trinh-saua-3x-2y-6b11x18y-1-52912.html
bạn vào đây xem nhé!
Hoc tốt!!!!!!!!!!!
Trl
-Bạn kia làm đúng rồi !~
Học tốt
nhé bạn :>
Cho hệ phương trình
x
3
-
y
3
-
x
2
y
+
x
y
2
-...
Đọc tiếp
Cho hệ phương trình x 3 - y 3 - x 2 y + x y 2 - 2 x y - x + y = 0 x - y = x 3 - 2 x 2 + y + 2 Số nghiệm của hệ phương trình là:
A. 2
B. 1
C. 0
D. 3
tìm nghiệm nguyên của phương trình
\(x^3-x^2y+3x-2y-5=0\) 0
giúp mk vs nha !
cảm ơn mn nhiều......
Tìm nghiệm nguyên của phương trình x2y+2y+5=3x+xy
Tìm nghiệm nguyên của phương trình sau
x3+x2y+2xy3=x2y2+y4
Tìm nghiệm nguyên dương của phương trình sau: 3x-2y=1
Em tham khảo ở đây:
Tìm nghiệm nguyên dương của phương trình sau: \(3^x-2^y=1\) - Hoc24
Đúng 3
Bình luận (0)
Tìm tất cả các nghiệm nguyên x, y của phương trình x3 + 2x2 + 3x + 2 = y3.
+, Nếu x = 0 => ko tồn tại y thuộc Z
+, Nếu x khác 0 => x^2 >= 1 => x^2-1 >= 0
Có : y^3 = x^3+2x^2+3x+2 > x^3 ( vì 2x^2+3x+2 > 0 )
Lại có : y^3 = (x^3+3x^3+3x+1)-(x^2-1) = (x+1)^3 - (x^2-1) < = (x+1)^3
=> x^3 < y^3 < = (x+1)^3
=> y^3 = (x+1)^3
=> x^2-1 = 0
=> x=-1 hoặc x=1
+, Với x=-1 thì y = 0
+, Với x=1 thì y = 2
Vậy .............
Tk mk nha
Đúng 1
Bình luận (0)
Ta có: \(x^3+2x^2+3x+2=y^3\) (1)
Xét \(2x^2+3x+2=2\left(x^2+\frac{3}{2}x\right)+2=2\left(x^2+\frac{3}{2}x+\frac{9}{16}\right)+2-2.\frac{9}{16}\)
\(=2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\) Vì \(\left(x+\frac{3}{4}\right)^2\ge0\Rightarrow2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\ge\frac{7}{8}>0\)
\(\Rightarrow y^3>x^3\Rightarrow y^3\ge\left(x+1\right)^3\)
\(\Rightarrow x^3+2x^2+3x+2\ge\left(x+1\right)^3\) \(\Rightarrow x^3+2x^2+3x+2\ge x^3+3x^2+3x+1\)
\(\Rightarrow x^3+3x^2+3x+1-x^3-2x^2-3x-2\le0\)
\(\Rightarrow x^2-1\le0\Rightarrow x^2\le1\) Vì \(x\in Z\Rightarrow\orbr{\begin{cases}x^2=1\\x^2=0\end{cases}}\)
+ TH1: x2 = 0 => x =0 Thay vào pt (1) ta được y3 = 2 (loại) vì y nguyên
+ TH2 : x2 = 1 => \(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Thay x=1 vào pt (1) ta đc: 1+2+3+2 = 8 = y3 => y = 2
Thay x= -1 vào pt (1) ta đc: -1 + 2 -3 +2 = 0 =y3 => y = 0
Vậy cặp (x;y) là (1;2) ; (-1;0).
Đúng 0
Bình luận (0)
\(Xét \(2x^2+3x+2=2\left(x+\dfrac{3}{4}\right)^2+\dfrac{7}{16}>0\forall x\in R\) => \(x^3< y^3\left(1\right)\) (1) Giả sử : \(y^3< \left(x+2\right)^3\) \(\Leftrightarrow x^3+2x^2+3x+2< x^3+6x^2+12x+8\) \(\Leftrightarrow-4x^2-9x-6< 0\) \(\Leftrightarrow4x^2+9x+6>0\) \(\Leftrightarrow4\left(x+\dfrac{9}{8}\right)^2+\dfrac{15}{64}>0\) => Giả sử đúng . => \(y^3< \left(x+2\right)^3\left(2\right)\) Từ (1)(2) => \(y^3=\left(x+1\right)^3\) \(\Leftrightarrow x^3+2x^2+3x+2=x^3+3x^2+3x+1\) \(\Leftrightarrow x^2=1\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\) .) Khi \(x=1\Rightarrow y=2\). .) Khi \(x=-1\Rightarrow y=0\) Vậy nghiệm của pt ( x;y ) = {( 1;2 ) ; ( -1;0 )}\)
Đúng 0
Bình luận (0)