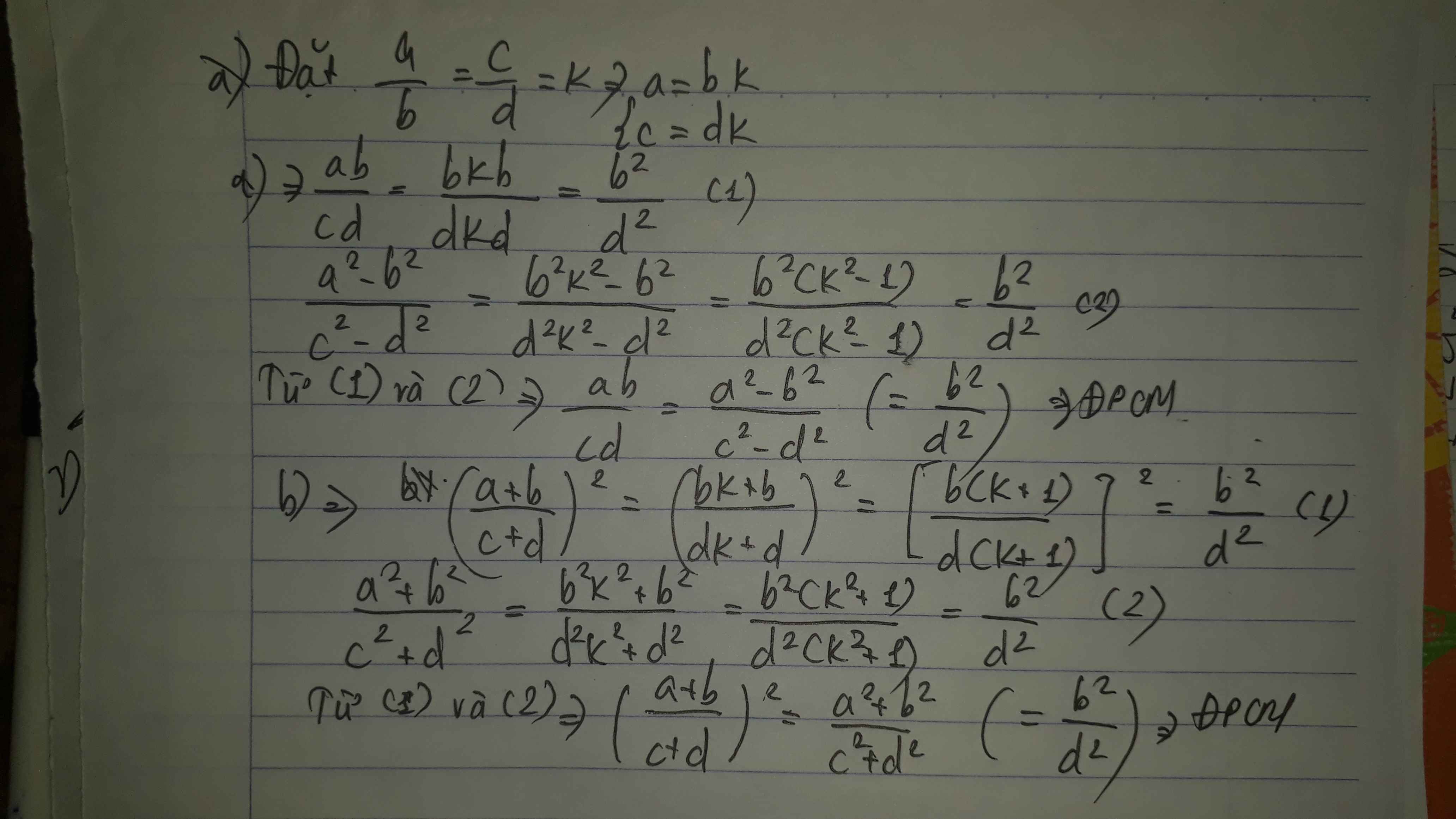bài này hình như sai đề rồi bn ơi ko thì viết lại đề giùm mk cái, khó đọc quá

đúng nha

Câu 1 

Ta có : \(\frac{a}{b}=\frac{c}{d}=>\left(\frac{a}{b}+1\right)=\left(\frac{c}{d}+1\right)\left(=\right)\frac{a+b}{b}=\frac{c+d}{d}\)

=> ĐPCM

Câu 2

Ta có \(\frac{a}{b}=\frac{c}{d}=>\frac{b}{a}=\frac{d}{c}=>\left(\frac{b}{a}+1\right)=\left(\frac{d}{c}+1\right)\left(=\right)\frac{b+a}{a}=\frac{d+c}{c}=>\frac{a}{b+a}=\frac{c}{d+c}\)

=> ĐPCM

Câu 3

Câu 3

Ta có \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)(=) (a+b).(c-d)=(a-b).(c+d)(=)ac-ad+bc-bd=ac+ad-bc-bd(=)-ad+bc=ad-bc(=) bc+bc=ad+ad(=)2bc=2ad(=)bc=ad=> \(\frac{a}{b}=\frac{c}{d}\)

=> ĐPCM

Câu 4 

Đặt \(\frac{a}{b}=\frac{c}{d}=k\)

\(=>\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)

Ta có \(\frac{ac}{bd}=\frac{bk.dk}{bd}=k^2\left(1\right)\)

Lại có \(\frac{a^2+c^2}{b^2+d^2}=\frac{b^2k^2+c^2k^2}{b^2+d^2}=\frac{k^2.\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)

Từ (1) và (2) => ĐPCM

Mày là thằng anh tuấn lớp 7c trường THCS yên lập đúng ko 

Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)

\(\frac{a^2-b^2}{ab}=\frac{\left(bk\right)^2-b^2}{bk.b}=\frac{b^2.k^2-b^2}{b^2k}=\frac{b^2\left(k^2-1\right)}{b^2k}=\frac{k^2-1}{k}\left(1\right)\)

\(\frac{c^2-d^2}{cd}=\frac{\left(dk\right)^2-d^2}{dk.d}=\frac{d^2k^2-d^2}{d^2k}=\frac{d^2\left(k^2-1\right)}{d^2.k}=\frac{k^2-1}{k}\left(2\right)\)

Từ (1) và (2)=>\(\frac{a^2-b^2}{ab}=\frac{c^2-d^2}{cd}\).

phần b đề kiểu gì vậy??//

        Lời giải

Ta có: \(\frac{a}{b}=\frac{b}{c}\Rightarrow\frac{a^2}{b^2}=\frac{b^2}{c^2}=\frac{a.b}{b.c}=\frac{a}{c}\) (1)

Mặt khác,áp dụng t/c tỉ dãy số bằng nhau,ta có:\(\frac{a^2}{b^2}=\frac{b^2}{c^2}=\frac{a^2+b^2}{b^2+c^2}\) (2)

Từ (1) và (2) ta có đpcm (điều phải chứng minh)

tth, Cảm ơn bạn nhìu!

đặt \(\frac{a}{b}=\frac{b}{c}=k\)=> a= bk; b= ck

xét:

+) \(\frac{a^2+b^2}{b^2+c^2}\)=\(\frac{b^2k^2+c^2k^2}{c^2k^2+c^2}\)=\(\frac{k^2\left(b^2+c^2\right)}{c^2\left(k^2+1\right)}\)=\(\frac{k^2\left(c^2k^2+c^2\right)}{c^2\left(k^2+1\right)}\)=\(\frac{k^2c^2\left(k^2+1\right)}{c^2\left(k^2+1\right)}\)=\(k^2\)

+) \(\frac{a}{c}\)=\(\frac{bk}{c}=\frac{ckk}{c}=k^2\)

=> \(\frac{a^2+b^2}{b^2+c^2}=\frac{a}{c}\)đpcm

Lần sau bạn cho thêm cả dấu ngoặc cho dễ hiểu nhé :v

Đặt \(\frac{a}{b}=\frac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) \(\left(b,d\ne0\right)\)

Thay \(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) vào \(\frac{a^2-b^2}{ab}\) và \(\frac{c^2-d^2}{cd}\) ta có :

\(\left\{{}\begin{matrix}\frac{\left(b.k\right)^2-b^2}{b.k.b}\\\frac{\left(d.k\right)^2-d^2}{d.k.d}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{b^2.k^2-b^2}{b^2.k}\\\frac{d^2.k^2-d^2}{d^2.k}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{b^2\left(k^2-1\right)}{b^2.k}\\\frac{d^2\left(k^2-1\right)}{d^2.k}\end{matrix}\right.\) <=>\(\left\{{}\begin{matrix}\frac{k^2-1}{k}\\\frac{k^2-1}{k}\end{matrix}\right.\)(vì b,d khác 0 nên \(b^2,d^2\) khác 0)

=> \(\frac{a^2-b^2}{ab}\) = \(\frac{c^2-d^2}{cd}\) (vì cùng bằng \(\frac{k^2-1}{k}\))

vậy \(\frac{a^2-b^2}{ab}\) = \(\frac{c^2-d^2}{cd}\) nếu \(\frac{a}{b}=\frac{c}{d}\)

lâu lắm không làm nên không chắc đâu :v