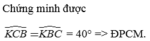Bài 4: Cho △ ABC có A = 60o , B =40o . Tia phân giác góc C cắt AB tại K. Cm: KB = KC

Những câu hỏi liên quan
Cho tam giác ABC có góc B = 60o , góc C = 40O tia phân giác của góc B cắt AC tại D, tia phân giác của C cắt AB tại BD và CK cắt nhau tại I. Tính góc DIK ?
giúp mình với
Cho tam giác ABC có A ^ = 60 ° , B ^ = 40 ° . Tia phân giác của góc C cắt cạnh AB tại K. Chứng minh KB = KC.
cho tam giác ABC có góc A =60 độ, B=40 độ . TIa phân giác của góc cắt AB ở K. CM KB=KC
Xét \(\Delta ABC\) có \(\widehat{B}=40^o,\widehat{A}=60^o\)
\(\Rightarrow\widehat{BCA}=80^o\)
Mà : CK là tia phân giác của góc \(\widehat{BCA}\)
\(\Rightarrow\widehat{BCK}=\widehat{ACK}=\frac{80^o}{2}=40^o\)
Xét \(\Delta BKC\) có : \(\widehat{KBC}=\widehat{KCB}=40^o\)
\(\Rightarrow\Delta BKC\) cân ở K
\(\Rightarrow KB=KC\) (đpcm)
Cho tam giác ABC vuông tại C biết CB = 8cm , AB = 10cm
a) Tính AC
b) Trên AB lấy điểm D sao cho AD = 6 cm . C/m : tam giác ACD cân
c) Tia phân giác góc A cắt CD và CB tại I và K . C/m : AI vuông góc với CD
d) So sánh độ dài KC và KB
Bài 1: Cho tam giác ABC vuông tại A. Vẽ đường phân giác BD ( D thuộc AC ). Kẻ AE vuông góc BD ( E thuộc BD ). Đường thẳng AE cắt BC tại K.
a) CM: tam giác BAK cân.
b) Cho DC =10cm, KC = 8cm. Tính DK.
c) Vẽ tia Ax so cho AK là tia phân giác góc CAx, tia Ax cắt BD tại I. Chứng minh KI vuông góc AB.
Bài 1. Cho △ABC vuông ở C, có A60^0, tia phân giác của góc BAC cắt BC ở E, kẻ EK vuông góc với AB ( K thuộc AB ), kẻ BD vuông góc với AE ( D thuộc AE )CMR: a, AKKB b, ADBCBài 2 Cho Δ ABC vuông tại A có BD là tia phân giác, kẻ DE vuông góc với BD (E thuộc BC). Gọi F là giao điểm của AB và DE. CMR: a, BD là đường trung trực của AEb, DFDCc, ADDCd, AE//FC
Đọc tiếp
Bài 1. Cho △ABC vuông ở C, có A=60\(^0\), tia phân giác của góc BAC cắt BC ở E, kẻ EK vuông góc với AB ( K thuộc AB ), kẻ BD vuông góc với AE ( D thuộc AE )
CMR: a, AK=KB b, AD=BC
Bài 2 Cho Δ ABC vuông tại A có BD là tia phân giác, kẻ DE vuông góc với BD (E thuộc BC). Gọi F là giao điểm của AB và DE. CMR:
a, BD là đường trung trực của AE
b, DF=DC
c, AD<DC
d, AE//FC
2:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
DE<DC
=>AD<DC
d: Xét ΔBFC co BA/AF=BE/EC
nên AE//CF
Đúng 0
Bình luận (0)
Bài 3 Cho hình thang vuông ABCD có A = D = 90 độ, I là trung điểm AD và CI là tia phân giác góc C. Gọi H là chân đường vuông góc kẻ từ I đến BC. CMR góc AHD bằng 90 độ và BIC bằng 90 độ và CMR AB+CD=BC
Bài 4: Cho tam giác ABC vuông tại A, AB = 14 cm, BC = 50 cm. Đường trung trực của AC cắt tia phân giác góc B ở K. CMR góc BKC vuông và tính độ dài KB
Vẽ hình giúp mik và làm giúp mình với:
Bài 2:
Cho △ABC ⊥ tại A, có góc B = 60o và AB = 5 cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E
a) C/m △ABC = △EBD
b) C/m △ABE là △đều
c) Tính độ dài AC
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE
=>ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
c: Xét ΔABC vuông tại A có
\(\tan B=\dfrac{AC}{AB}\)
\(\Leftrightarrow AC=5\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác abc có góc A bằng 60 độ các tia phân giác trong của góc B và C cắt tại I , các tia phân giác ngoài của góc B và C cắt nhau tại K . tia BI cắt KC tại D. Tính góc BIC , góc BKC , CMR góc BDC= BAC /2