trong hai hình tam giác ABCD và EFGH sau có tam giác nào bằng nhau vì sao

Những câu hỏi liên quan
Cho hình bên, trong đó ABCD là hình thang.a, Trong hình thang đó những tam giác nào có diện tích bằng nhau? Vì sao?b, Biết chiều cao của tam giác OBC kẻ từ O bằng chiều cao của hình thang ABCD. Hãy tìm trong hình thang đó xem những tam giác nào có diện tích bằng diện tích hình tam giác OBC. Vì sao?
Đọc tiếp
Cho hình bên, trong đó ABCD là hình thang.
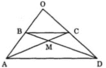
a, Trong hình thang đó những tam giác nào có diện tích bằng nhau? Vì sao?
b, Biết chiều cao của tam giác OBC kẻ từ O bằng chiều cao của hình thang ABCD. Hãy tìm trong hình thang đó xem những tam giác nào có diện tích bằng diện tích hình tam giác OBC. Vì sao?
a, Diện tích BAD = diện tích CAD (chung đáy AD, các đường cao vẽ từ B, C đến AD bằng nhau)
Diện tích ABC = diện tích BDC (chung đáy BC, các đường cao vẽ từ A và D đến BC bằng nhau)
Suy ra diện tích ABM bằng diện tích DCM
b, Diện tích ABC = diện tích DBC = diện tích OBC (chung đáy BC và 3 đường cao vẽ từ A, D, O đến BC bằng nhau)
Đúng 1
Bình luận (0)
trong các hình tam giác sau có tam giác nào bằng nhau vì sao
Không có hình thì làm sao ?
không có hình tam giác nào thì bố mày làm được
Cho hình thang ABCD
a) trong hình thang này, những tam giác nào nào có diện tích bằng nhau. Vì sao?
b) biết đường cao của tam giác OBC ( vẽ từ O bằng đường cao của hình thang. Hãy tìm những tam giác có diện tích bằng OBC? Vì sao?
VẼ HÌNH HỘ MÌNH NHA
Bài 1: Cho hình bình hành ABCD, các tia phân giác của góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.a, Tứ giác EFGH là hình gì? Vì sao?b, CM: EG FH c, Hình bình hành ABCD phải thêm điều kiện gì để EFGH là hình vuôngBài 2: Cho tam giác ABC, về phía ngoài của tam giác vẽ 2 hình vuông ABEF và ACGH. CMR: Đường thẳng BG và Ce cắt nhau tại 1 điểm nằm trên đường AD của tam giác ABC
Đọc tiếp
Bài 1: Cho hình bình hành ABCD, các tia phân giác của góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.
a, Tứ giác EFGH là hình gì? Vì sao?
b, CM: EG = FH
c, Hình bình hành ABCD phải thêm điều kiện gì để EFGH là hình vuông
Bài 2: Cho tam giác ABC, về phía ngoài của tam giác vẽ 2 hình vuông ABEF và ACGH.
CMR: Đường thẳng BG và Ce cắt nhau tại 1 điểm nằm trên đường AD của tam giác ABC
Cho hình vẽ bên ABCD là hình thang vuông.
a) Trong hình thang có những tam giác nào có diện tích bằng nhau ? Vì sao ?
b) Biết chiều cao của tam giác ODC ( vẽ từ điểm O ) bằng chiều cao của hình thang ABCD. Có những hình nào có diện tích bằng diện tích tam giác ODC
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh lấy trong số các điểm A, B, C, O, hãy chỉ ra các tam giác có diện tích bằng nhau và giải thích vì sao.
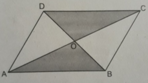
Xem hình bs.52.
- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.
- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.
Đúng 0
Bình luận (0)
Cho hình thang \(ABCD\) có hai đáy là \(AB\), \(CD\) và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua \(C\), song song với \(BD\) và cắt \(AB\) tại \(E\).
a) Tam giác \(CAE\) là tam giác gì? Vì sao?
b) So sánh tam giác \(ABD\) và tam giác \(BAC\)
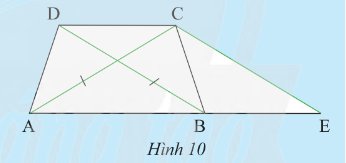
a) Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AB\;{\rm{//}}\;CD\)
Xét \(\Delta BCD\) và \(\Delta CBE\) ta có:
\(\widehat {DCB} = \widehat {CBE}\) (do \(AB\) // \(CD\))
\(BC\) chung
\(\widehat {CBD} = \widehat {BCE}\) (do \(CE\) // \(BD\))
Suy ra \(\Delta BCD = \Delta CBE\) (g-c-g)
Suy ra \(BD = CE\) (hai cạnh tương ứng)
Mà \(AC = BD\) (cmt)
Suy ra \(AC = EC\)
Suy ra \(\Delta CAE\) cân tại \(C\)
b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:
\(DA = BC\) (do \(ABCD\) là hình thang cân)
\(\widehat {DAB} = \widehat {CBA}\) (Do \(ABCD\) là hình thang cân)
\(AB\) chung
Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.
a) Tứ giác EFGH là hình gì ? Vì sao ?
b) Chứng minh rằng EG = FH và bằng hiệu giữa hai cạnh kề một đỉnh của hình bình hành ABCD.
c) Hình bình hành ABCD cần có thêm điều kiện gì để EFGH là hình vuông?
Cho hình bình hành ABCD các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH. CMR:
a, Tứ giác EFGH là hình gì? Vì sao?
b, EG = FH và bằng hiệu giữa hai cạnh kề của hình bình hành ABCD
c, Hình bình hành ABCD cần điều kiện gì để EFGH là hình vuông?















