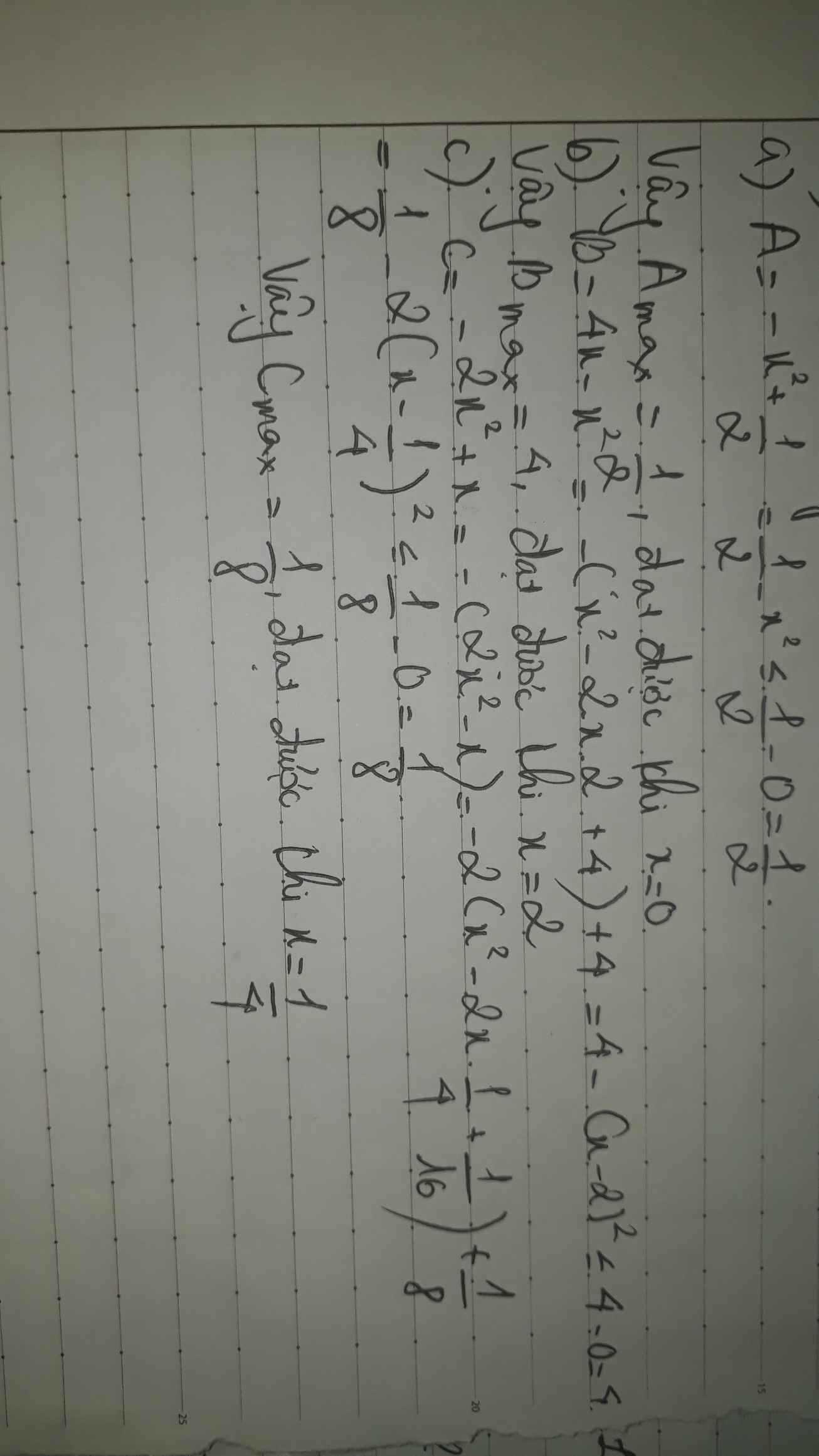bài 1)tìm GTLN của biểu thức D=2x^2+4x-1/x^2+x+1
Những câu hỏi liên quan
bài 1)tìm GTLN của biểu thức D=2x^2+4x-1/x^2+x+1
Bài 1:Tìm giá trị nhỏ nhất của các biểu thức sau:
F= (3x^2-6x+17)/(x^2-2x+5)
H= (x^2-4x+1)/x^2
Bài 2:Tìm GTNN và GTLN cua biểu thức sau:
D= (3x^2-2x+3)/(x^2+4)
Tìm GTNN của biểu thức A= x^2-6x+10; B= 3x^2-12x+1; Tìm GTLN của biểu thức C= -x^2+2x+5; D= 4x-x^2; E = x.(x-3)(x-4)(x-7)
\(A=x^2-6x+10\)
\(\Leftrightarrow A=x^2-2\cdot x\cdot3+3^2-9+10\)
\(\Leftrightarrow A=\left(x-3\right)^2+1\ge1\) \(\forall x\in z\)
\(\Leftrightarrow A_{min}=1khix=3\)
\(B=3x^2-12x+1\)
\(\Leftrightarrow B=\left(\sqrt{3}x\right)^2-2\cdot\sqrt{3}x\cdot2\sqrt{3}+\left(2\sqrt{3}\right)^2-12+1\)
\(\Leftrightarrow B=\left(\sqrt{3}x-2\sqrt{3}\right)^2-11\ge-11\) \(\forall x\in z\)
\(\Leftrightarrow B_{min}=-11khix=2\)
Đúng 0
Bình luận (0)
tìm gtln của các biểu thức sau
a)A=-x^2+1/2
b)B=4x-x^2
c)C=-2x^2+x
d)D=4/3x-2x^2-1
e)E=4xy+4y+2x-2x^2-4x^2-6
Thật ra cách làm dạng bài này cũng gần giống như bài tìm gtnn bạn vừa hỏi, chỉ khác ở chỗ đặt dấu âm ra ngoài để tìm được gtln thôi.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Tìm GTNN của biểu thức: căn x(căn x-2)/ 1+ căn x
Bài 2: Tìm GTLN của biểu thức: căn x+3/4x
Tìm GTLN của biểu thức:
A=-x^2+6x-15
B=-2x^2+8x-15
C=-3^2+2x-1
D=-5x^2-25x+49
Tìm GTNN của biểu thức:
A=x^2-4x+7
B=x^2+8x
C=2x^2+4x+15
D=3x^2-2x-1
Tìm GTLN:
\(A=-x^2+6x-15\)
\(=-\left(x^2-6x+15\right)\)
\(=-\left(x^2-2.x.3+9+6\right)\)
\(=-\left(x+3\right)^2-6\le0\forall x\)
Dấu = xảy ra khi:
\(x-3=0\Leftrightarrow x=3\)
Vậy Amax = - 6 tại x = 3
Tìm GTNN :
\(A=x^2-4x+7\)
\(=x^2+2.x.2+4+3\)
\(=\left(x+2\right)^2+3\ge0\forall x\)
Dấu = xảy ra khi:
\(x+2=0\Leftrightarrow x=-2\)
Vậy Amin = 3 tại x = - 2
Các câu còn lại làm tương tự nhé... :)
Đúng 0
Bình luận (0)
Tìm GTLN - GTNN của các biểu thức ?* bài 1: Tìm GTNN: a) A (x - 5)² + (x² - 10x)² - 24 b) B (x - 7)² + (x + 5)² - 3 c) C 5x² - 6x +1 d) D 16x^4 + 8x² - 9 e) A (x + 1)(x - 2)(x - 3)(x - 6) f) B (x - 2)(x - 4)(x² - 6x + 6) g) C x^4 - 8x³ + 24x² - 8x + 25 h) D x^4 + 2x³ + 2x² + 2x - 2 i) A x² + 4xy + 4y² - 6x – 12y +4 k) B 10x² + 6xy + 9y² - 12x +15 l) C 5x² - 4xy + 2y² - 8x – 16y +83 m) A (x - 5)^4 + (x - 7)^4 – 10(x - 5)²(x - 7)² + 9 * Bài 2: Tìm GTLN: a) M -7x² + 4x -12 b) N -16x² - 3x +14 c) M...
Đọc tiếp
Tìm GTLN - GTNN của các biểu thức ?
* bài 1: Tìm GTNN:
a) A= (x - 5)² + (x² - 10x)² - 24
b) B= (x - 7)² + (x + 5)² - 3
c) C= 5x² - 6x +1
d) D= 16x^4 + 8x² - 9
e) A= (x + 1)(x - 2)(x - 3)(x - 6)
f) B= (x - 2)(x - 4)(x² - 6x + 6)
g) C= x^4 - 8x³ + 24x² - 8x + 25
h) D= x^4 + 2x³ + 2x² + 2x - 2
i) A= x² + 4xy + 4y² - 6x – 12y +4
k) B= 10x² + 6xy + 9y² - 12x +15
l) C= 5x² - 4xy + 2y² - 8x – 16y +83
m) A= (x - 5)^4 + (x - 7)^4 – 10(x - 5)²(x - 7)² + 9
* Bài 2: Tìm GTLN:
a) M= -7x² + 4x -12
b) N= -16x² - 3x +14
c) M= -x^4 + 4x³ - 7x² + 12x -5
d) N= -(x² + x – 2) (x² +9x+18) +27
* Bài 3:
1) Cho x - 3y = 1. Tìm GTNN của M= x² + 4y²
2) Cho 4x - y = 5. Tìm GTNN của 3x²+2y²
3) Cho a + 2b = 2. Tìm GTNN của a³ + 8b³
* Bài 4: Tìm GTLN và GTNN của các biểu thức:
1) A = (3 - 4x)/(x² + 1)
2) B= (8x + 3)/(4x² + 1)
3) C= (2x+1)/(x²+2)
Toán lớp 1 cái gì,xạo.Toán trung học thì có.
Đúng 0
Bình luận (2)
Lớp 1 mà làm được cái này thì...THIÊN TÀI
Đúng 4
Bình luận (0)
tìm gtln của các biểu thức sau
a)A=-x^2+1/2
b)B=4x-x^2
c)C=-2x^2+x
d)D=4/3x-2x^2-1
e)E=4xy+4y+2x-2x^2-4x^2-6
giúp mik nha mik đang rất gấp!
Tìm GTLN và GTNN của biểu thức sau : 4x+1/ x^2+2x+2
là \(4x+\dfrac{1}{x^2}+2x+2\) hay là \(\dfrac{4x+1}{x^2+2x+2}\) cái neog:0
Đúng 0
Bình luận (1)
\(P=\dfrac{4x+1}{x^2+2x+2}=\dfrac{x^2+2x+2-x^2+2x-1}{x^2+2x+2}=1-\dfrac{\left(x-1\right)^2}{x^2+2x+2}\le1\)
"=" xảy ra <=> x - 1 = 0 <=> x = 1
Vậy Max P = 1 <=> x = 1
P = \(\dfrac{4x+1}{x^2+2x+2}=\dfrac{-4x^2-8x-8+4x^2+12x+9}{x^2+2x+2}=-4+\dfrac{\left(2x+3\right)^2}{x^2+2x+2}\)
\(\ge-4\)
"=" xảy ra <=> 2x + 3 = 0 <=> x = -1,5
Vậy Min P = -4 <=> x = -1,5
Đúng 1
Bình luận (0)