cho tam giác ABC vuông tại A đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MA =MD
a) cmr; tam giác AMC =tam giác DMB
b) góc ABD =?
c)cmr AM=\(\frac{1}{2}\)
Những câu hỏi liên quan
cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a. Tính số đo góc ABD.
b. Chứng minh ΔABC = ΔBAD
c. So sánh độ dài AM và BCho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o.
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Đúng 5
Bình luận (0)
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o.
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh ΔABC = ΔBAD
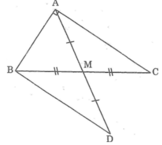
Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. So sánh độ dài AM và BC.
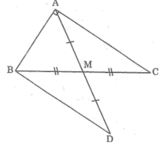
Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A cóAB<AC, đường trung tuyến AM. trên tia đối của tia MA lấy điểm D sao cho MD=MA a) chứng minh tam giác MAC = tam giác MDB b) chứng minh BD vuông góc với AB vad AM=1/2BC
a: Xét ΔMAC và ΔMDB có
MA=MD
góc AMC=góc DMB
MC=MB
=>ΔMAC=ΔMDB
b: ΔMAC=ΔMDB
=>góc MAC=góc MDB
=>AC//DB
=>DB vuông góc AB
ΔABC vuông tại A
mà AM là trung tuyến
nên AM=1/2BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Tính số đo góc ABD.
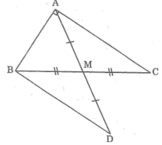
Xét ΔAMC và ΔDMB, ta có:
CM = BM (gt)
∠(AMC) = ∠(BMD) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy ∠(ABD) = 90o.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, ABC > ACB, trung tuyến AM . Trên tia đố của tia CB lấy điểm D sao cho C là trung điểm của MD . Trên tia đối của tia BA lấy điểm E sao cho BE=BA Trên tia đối của tia MA lấy điểm N sao cho
MN=MA.
a) Chứng minh tam giác AMB bằng tam giác NMC và NC vuông góc với AC ;
b) Gọi I là trung điểm của DE . Chứng minh ba điểm A, M, I thẳng hàng
c*) So sánh AD và BC.
a/
Xét tg AMB và tg MNC có
MB=MC (giả thiết)
MA=MN (giả thiết)
\(\widehat{AMB}=\widehat{NMC}\) (góc đối đỉnh)
=> tg AMB = tg NMC (c.g.c)
b/ Nối A với I cắt BD tại M'
Xét tg ADE có
BE=BA (gt) => DE là trung tuyến của tg ADE
IE=ID (gt) => AI là trung tuyến của tg ADE
=> M' là trọng tâm của tg ADE => \(BM'=\dfrac{1}{3}BD\) (1)
Ta có
MB=MC (gt); MC=CD (gt) => MB=MC=CD
BD=MB+MC+CD
=> \(BM=\dfrac{1}{3}BD\) (2)
Từ (1) và (2) => \(M'\equiv M\)
=> A; M; I thẳng hàng
Đúng 0
Bình luận (0)
Co tam giác ABC vuông tại A Lấy đường trung tuyến Am .Trên tia đối của tia MA lấy điểm D sao cho MD=MA a) tính góc ABD b) chứng minh tam giác ABC = tam giacs BAD c) chứng minh AM =1/2 BC
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
Tính số đo góc ABD
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a, chứng minh △AMB=△DMC
b, trên tia đối của tia CD, lấy điểm T sao cho CI=CA, qua điểm I vẽ đường thẳng song song AC cắt AB tại E. chứng minh △ACE là △ vuông cân
Giúp mình với ạaaa :3
cho tam giác abc vuông tại a,đường trung tuyến am. trên tia đối của tia ma lấy điểm d sao cho md =mà.tính số đo góc abd