cho 2 dây AB và CD của đường tròn O cắt nhau tại M . chứng minh MA.MB=MC.MD

Những câu hỏi liên quan
mn ơiiiii giúp mik ý 2 vs ạ rất gấp lun í
Cho đường tròn (O) và một điểm M thuộc miền trong của (O). Vẽ AB; CD là hai dây cung tùy ý của đường tròn mà cắt nhau tại M. Chứng minh rằng MA.MB = MC.MD =R^2-OM^2
Cho tứ giác ABCD nội tiếp đường tròn (O) (ABCD không phải là hình thang). AB cắt CD tại M. So sánh MA.MB và MC.MD
Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
Đúng 0
Bình luận (0)
hát chế con nợ mẹ(tớ nợ cậu một câu trả lời,vì kiếp này tôi mới học lớp 5)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho (o;R) và một điểm M bên trong đường tròn (o). Qua M kẻ 2 dây AB và CD vuông góc với nhau ( c thuộc cung nhỏ AB). vẽ đường kính DE. chứng minh
a, MA.MB=MC.MD
b, tứ giác ABEC là hình thang cân
c, tổng MA^2+MB^2+MC^2+MD^2; AB^2+CD^2 ko đổi
d, tìm vị trí của AB và CD để AC+BD, diện tích tg ABCD min, max
cho đường tròn ( O, R) có hai dây AB và CD vuông góc với nhau tại H ( AB và CD không đi qua tâm O, điểm C thuộc cung nhỏ AB). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng CD tại M, vẽ CK vuông góc với AM tại K.Gọi N là giao điểm của AO và CD.
a) Chứng Minh AHCK là tứ giác nội tiếp.
b) Chứng minh HK song song với AD và MH.MN=MC.MD
c) Tính HA2+HB2+HC2+HD2 theo R
a) Từ một điểm M ở bên ngoài đường tròn left(O;Rright)kẻ tiếp tuyến MT và hai cát tuyến MAB và MCD với đường tròn (O) left(A,B,C,Dinleft(Oright)right). Chứng minh MA.MBMC.MDMT^2OM^2-R^2b) Qua điểm M ở bên trong đường tròn left(O;Rright)kẻ hai dây cung AB và CD của đường tròn (O) left(A,B,C,Dinleft(Oright)right).Chứng minhMA.MBMC.MDR^2-OM^2
Đọc tiếp
a) Từ một điểm M ở bên ngoài đường tròn \(\left(O;R\right)\)kẻ tiếp tuyến MT và hai cát tuyến MAB và MCD với đường tròn (O) \(\left(A,B,C,D\in\left(O\right)\right)\). Chứng minh \(MA.MB=MC.MD=MT^2=OM^2-R^2\)
b) Qua điểm M ở bên trong đường tròn \(\left(O;R\right)\)kẻ hai dây cung AB và CD của đường tròn (O) \(\left(A,B,C,D\in\left(O\right)\right).\)Chứng minh\(MA.MB=MC.MD=R^2-OM^2\)
Cho đường tròn O và một 1 điểm M nằm ngoài đường tròn. Qua M vẽ 2 tiếp tuyến MA, MB (A,B là các tiếp điểm). Vẽ các tuyến MCD với đường tròn (MCMD). Gọi I là trung điểm dây CDa/ Chứng minh 5 điểm M, A, I, O, C cùng thuộc một đường tròn.b/ Dây AB cắt OM tại H. Chứng minh tứ giác OHCD nội tiếp.c/ Gọi K là giao điểm của AB với CD. Chứng minh tứ giác OIKH nội tiếp được suy ra MK.MI MC.MD
Đọc tiếp
Cho đường tròn O và một 1 điểm M nằm ngoài đường tròn. Qua M vẽ 2 tiếp tuyến MA, MB (A,B là các tiếp điểm). Vẽ các tuyến MCD với đường tròn (MC<MD). Gọi I là trung điểm dây CD
a/ Chứng minh 5 điểm M, A, I, O, C cùng thuộc một đường tròn.
b/ Dây AB cắt OM tại H. Chứng minh tứ giác OHCD nội tiếp.
c/ Gọi K là giao điểm của AB với CD. Chứng minh tứ giác OIKH nội tiếp được suy ra MK.MI = MC.MD
Cho đường tròn (O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O; OK) cắt KA và KC tại M và N. Chứng minh rằng KM < KN.
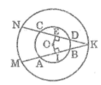
Kẻ OI ⊥ AB, OE ⊥ CD
Trong (O; OA) ta có: AB < CD (gt)
Suy ra : OI > OE (dây lớn hơn gần tâm hơn)
Trong (O ; OK) ta có : OI > OE (cmt)
Suy ra : KM < KN (dây gần tâm hơn thì lớn hơn)
Đúng 0
Bình luận (0)
Cho đường tròn (O), hai dây AB, CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết AB > CD, chứng minh rằng MH > MK.
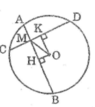
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM
Đúng 0
Bình luận (0)
Cho đường tròn tâm O có 2 dây AB và CD cắt nhau tại P. Gọi M, N theo thứ tự là trung điểm của AB và CD. Chứng minh rằng nếu AB>CD thì PM>PN













