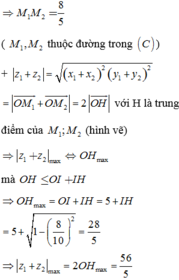Tìm nghiệm bất phương trình Ix - 3I < = 6

Những câu hỏi liên quan
Ix-3I - Ix-2I=3
Giải phương trình
Cho bất phương trình x + 6 + m > x 6 − 3 . Tìm m để bất phương trình có nghiệm x = 3.
giải phương trình: Ix-3I - 5x =7
pt <=> |x-3| = 7+5x
<=> x-3 = 7+5x hoặc x-3 = -7-5x
<=> x= -5/2 hoặc x = -2/3
Đúng 0
Bình luận (0)
Câu 1:Tìm nghiệm của bất phương trình x²-5x-6-6|x+1|≤0
Câu 2: Giải bất phương trình|x²-3|+2x≥0
Xem chi tiết
Giải phương trình Ix2 - 2x - 3I = x2 + I2x + 3I
Cho
z
1
,
z
2
là nghiệm phương trình
6
−
3
i
+
i
z
2
z
−
6
−
9
i
và thỏa mãn
z...
Đọc tiếp
Cho z 1 , z 2 là nghiệm phương trình 6 − 3 i + i z = 2 z − 6 − 9 i và thỏa mãn z 1 − z 2 = 8 5 . Tìm giá trị lớn nhất của z 1 + z 2 .
A. 56 5
B. 28 5
C. 6
D. 5
Cho
z
1
,
z
2
là nghiệm phương trình
6
−
3
i
+
i
z
2
z
−
6
−
9
i
và thỏa mãn
z...
Đọc tiếp
Cho z 1 , z 2 là nghiệm phương trình 6 − 3 i + i z = 2 z − 6 − 9 i và thỏa mãn z 1 − z 2 = 8 5 . Tìm giá trị lớn nhất cảu z 1 + z 2 .
A. 56 5
B. 28 5
C. 6
D. 5
Đáp án A.
Đặt z = x + y i với x , y ∈ ℝ ; z 1 = x 1 + y 1 i ; z 2 = x 2 + y 2 i
6 − 3 i + i z = 2 z − 6 + 9 i ⇔ x 2 + y 2 − 6 x + 8 y + 24 = 0
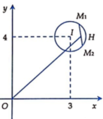
Tập hợp điểm điểm biểu diễn z là đường tròn (C) tâm I 3 ; 4 và bán kính R=1.
+ Có z 1 − z 2 = x 1 − x 2 2 + y 1 − y 2 2 = M 1 M 2 → với M 1 x 1 ; y 1 là điểm biểu diễn số phức z 1 , M 2 x 2 ; y 2 là điểm biểu diễn số phức z 2
⇒ M 1 M 2 = 8 5 ( M 1 , M 2 thuộc đường trong C )
z 1 + z 2 = x 1 + x 2 2 y 1 + y 2 2 = O M 1 → + O M 2 → = 2 O H → với H là trung điểm của M 1 ; M 2 (hình vẽ)
⇒ z 1 + z 2 max ⇔ O H max mà O H ≤ O I + I H
⇒ O H max = O I + I H = 5 + I H = 5 + 1 − 8 10 2 = 28 5 ⇒ z 1 + z 2 max = 2 O H max = 56 5
Đúng 0
Bình luận (0)
Tìm x
a, 2 Ix-3I-5=3
b, 2 I2x+3I + I2x+3I=6
c, 3 Ix+1I^2 + Ix+1I^2=16
a ) 2|x - 3| - 5 = 3 <=> 2|x - 3| = 8 <=> |x - 3| = 4 => x - 3 = ± 4
TH1 : x - 3 = 4 => x = 7
TH2 : x - 3 = - 4 => x = - 1
Vậy x = { - 1; 7 }
b ) 2|2x + 3| + |2x + 3| = 6 <=> 3|2x + 3| = 6 => |2x + 3| = 2 => 2x + 3 = ± 2
=> x = { - 5/2 ; - 1/2 }
c ) 3|x + 1|2 + |x + 1|2 = 16
4|x + 1|2 = 16
=> |x + 1|2 = 4 = 22 ( ko xét TH |x + 1| = - 2 vì |x + 1| ≥ 0 )
=> |x + 1| = 2 => x + 1 = ± 2 => x = { - 3; 1 }
Đúng 0
Bình luận (0)
Tìm tập nghiệm của bất phương trình
9
x
-
5
.
3
x
+
6
0
Đọc tiếp
Tìm tập nghiệm của bất phương trình 9 x - 5 . 3 x + 6 < 0
![]()
![]()
![]()
![]()