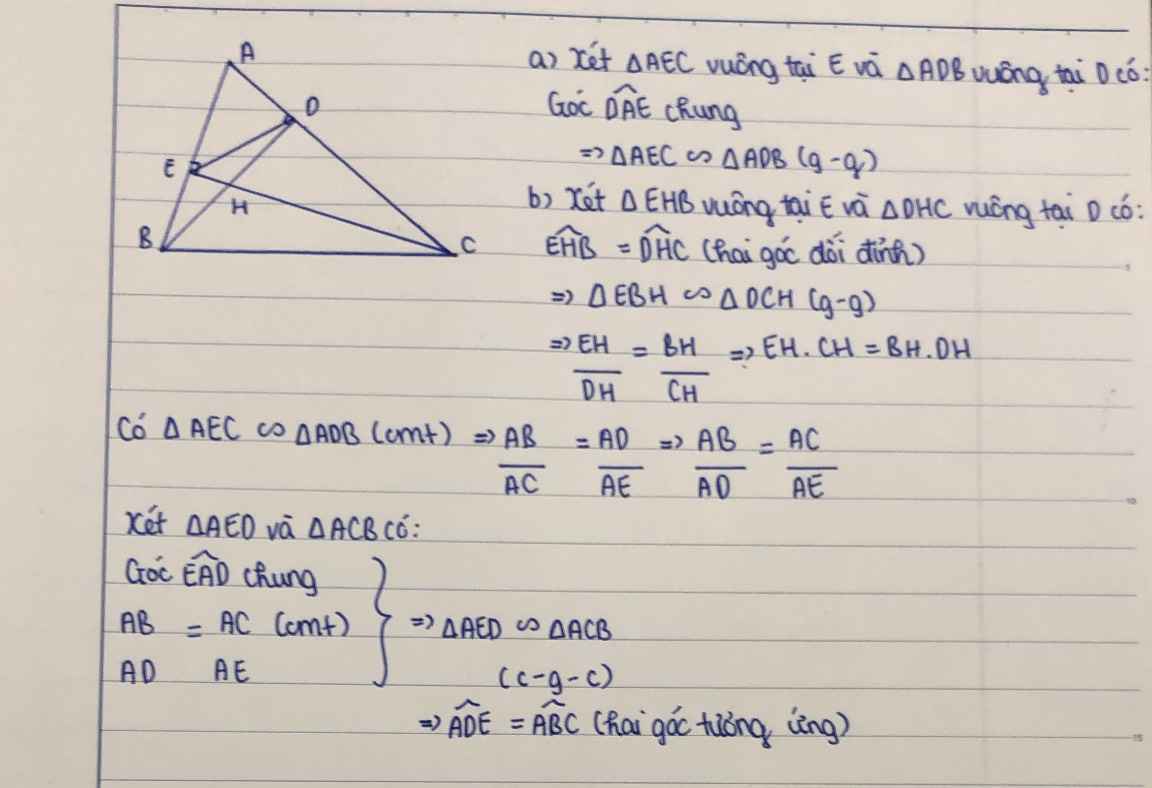cho tam giác ABC AD BK CL là ccas đường cao chứng minh tam giác AKL đồng dangj vs tam giác ABC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A đường cao AH. Vẽ đường phân giác AD của tam giác CHA , đường phân giác BK của tam giác ABC. Gọi giao của BK và AH, AD lần lượt là E và F. a) chứng minh tam giác AHB đồng dạng với tam giác CHA b) chứng minh tam giác AEF đồng dạng với tam giác BEH c) chứng minh KD //AH d) eh/ad = ed/dc
a: Xét ΔAHB vuông tại H và ΔCHA vuông tạiH có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
c: BK là phân giác
=>AK/CK=BA/BC
ΔAHC có AD là phân giác
nên DH/CD=AH/AC=BA/BC
=>DH/CD=AK/CK
=>KD//AH
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH
a/ chứng minh tam giác AHB đồng dạng tam giác CBA
b/ kẻ phân giác AD của tam giác CHA và đường phân giác BK của tam giác ABC, BK cắt AH và AD lần lượt tại E và F. Chứng minh tam giác AEF đồng dạng tam giác BEH
c/ KD//AH
d/ chứng minh EH/AB=KD/BC
a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{CBA}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB(g-g)
Đúng 0
Bình luận (0)
Cho tam giác ABC ccas góc đều nhọn. Các đường cao BD và CE cắt nhau tại A
a) Chứng minh tam giác ABD đồng dạng tam giác ABE
b) Chứng minh HBHD=HC x HE, góc ADE=góc ABC
a, Xét Δ ABD và Δ ABE, có :
\(\widehat{ADB}=\widehat{AEB}=90^o\)
\(\widehat{BAD}=\widehat{BAE}\) (góc chung)
=> Δ ABD ∾ Δ ABE (g.g)
b, Xét Δ EHB và Δ DHC, có :
\(\widehat{EHB}=\widehat{DHC}\) (đối đỉnh)
\(\widehat{HEB}=\widehat{HDC}=90^o\)
=> Δ EHB ∾ Δ DHC (g.g)
=> \(\dfrac{EH}{DH}=\dfrac{HB}{HC}\)
=> \(HB.HD=HC.HE\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ đường phân giác AD của tam giácCHA và đường phân giác BK của tam giác ABC (D thuộc BC; K thuộc AC). BK cắt lần lượt AH và AD tại E và F.a) Chứng minh: tam giác AHB đồng dạng với tam giác CHA. b) Chứng minh:tam giác AEF đồng dạng tam giác BEH .c) Chứng minh: KD // AH. d) Chứng minh:EH/AB KD/BCGIÚP VỚI !!! ( CHỨNG MINH CHI TIẾT NHÉ )
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ đường phân giác AD của tam giác![]() CHA và đường phân giác BK của tam giác ABC (D thuộc BC; K thuộc AC). BK cắt lần lượt AH và AD tại E và F.
CHA và đường phân giác BK của tam giác ABC (D thuộc BC; K thuộc AC). BK cắt lần lượt AH và AD tại E và F.
a) Chứng minh: ![]() tam giác AHB đồng dạng với tam giác CHA.
tam giác AHB đồng dạng với tam giác CHA.
b) Chứng minh:![]() tam giác AEF đồng dạng tam giác BEH .
tam giác AEF đồng dạng tam giác BEH .
c) Chứng minh: KD // AH.
d) Chứng minh:EH/AB = KD/BC
GIÚP VỚI !!! ( CHỨNG MINH CHI TIẾT NHÉ )
Cho tam giác ABC vuông tại A có AH là đường cao.
a) chứng minh tam giác AHB đồng dạng với CHA
b) Kẻ AD là phân giác của tam giác CHA; BK là phân giác của tam giác ABC. BK lần lượt cắt AH, AD tại E và F. Chứng minh tam giác AEF đồng dạng với BEH.
c) KD//AH
d) EH/AB = KD/BC
*giúp mình câu d với ạ!
Thanks.
Cho tam giác ABC vuông tại A, đường cao AH.a) Chứng minh: tam giác AHB ~ tam giác CHA.b) Kẻ đường phân giác AD của tam giác CHA và đường phân giác BK của tam giác ABC (D thuộc BC; K thuộc AC). BK cắt lần lượt AH và AD tại E và F. Chứng minh:tam giác AEF ∽ tam giác BEH .c) Chứng minh: KD // AH.d) Chứng minh: EH/AB =KD/BC
Cho tam giác ABC (AB<AC) có 2 đường cao AH,BK cắt nhau tại I. Qua B kẻ đường thẳng vuông góc với AB cắt AH tại E
A. Chứng minh tam giác BIA đồng dạng tam giác HIK và BKH=HBE
B. Kẻ phân giác AD của tam giác ABC. Chứng minh :IB/IE=AH/BK
Cho tam giác nhọn ABC nội tiếp trong đường tròn (O), AB < AC. Kẻ đường cao AH của tam giác. H thuộc BC và đường kính AD của đường tròn (O).
1. Chứng minh rằng tam giác BAH đồng dạng tam giác DAC.
2. Kẻ BK vuông góc AD, K thuộc AD. Chứng minh rằng tứ giác ABHK nội tiếp.
3. Chứng minh rằng đường thẳng HK vuông góc AC.
Gọi AM, BN, CL lần lượt là ba đường cao của tam giác ABC. Chứng minh: Tam giác ANL và tam giác ABC đồng dạng
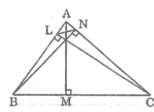
a. Xét hai tam giác BNA và CLA, ta có:
∠ BNA = ∠ CLA = 90 °
góc A chung
Suy ra ∆ BNA đồng dạng ∆ CLA (g.g)
Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB
Xét hai tam giác ABC và ANL, ta có:
AL/AC = AN/AB
góc A chung
Suy ra ∆ ABC đồng dạng ∆ ANL (c.g.c)
Đúng 0
Bình luận (0)