Vào link này nhé !!!

Câu hỏi của Võ Văn Phúc Đường - Toán lớp 7 - Học toán với OnlineMath

Mik cần hai cách mà bạn

-Tam giác ABC cân tại A  có BE và CD là 2 đtt

=> AB=AC => AE=AD

Xét tgABE , tgACD có góc A chung , AE=AD,AB=AC

=> ABE=ACD (c g c)

=>BE=CD

-Tam giác ABC có BE và CD là 2 đtt bằng nhau và cắt tại G

=> EG=DG , BG=CG

\(\Delta DGB\),\(\Delta EGC\) có gocDGB = gocEGC ( 2 góc đối đình) EG=DG, BG=CG

=>\(\Delta DGB\)=\(\Delta EGC\)(c.g.c)

=>BD=EC

Xét \(\Delta EBC\) và \(\Delta DCB\)  có: BE=CD , BC chung, BD=EC

=>\(\Delta EBC\)=\(\Delta DCB\) (c.c.c)

=>\(\widehat{EBC}=\widehat{DCB}\)

=> TgABC cân tại A (đpcm)

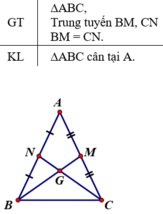
Giả sử ΔABC có hai đường trung tuyến BM và CN cắt nhau tại G.

⇒ G là trọng tâm của tam giác

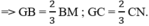
Mà BM = CN (theo gt) ⇒ GB = GC ⇒ GM = GN.

Xét ΔGNB và ΔGMC có :

GN = GM (cmt)

GB = GC (cmt)

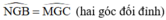
⇒ ΔGNB = ΔGMC (c.g.c) ⇒ NB = MC.

Lại có AB = 2.BN, AC = 2.CM (do M, N là trung điểm AC, AB)

⇒ AB = AC ⇒ ΔABC cân tại A.

 Giả sử ∆ABC  có hai đường trung tuyến BM và CN gặp nhau ở G => G là trọng tâm của tam giác  => GB = BM; GC = CN  mà BM = CN (giả thiết) nên GB = GC => ∆GBC cân tại G =>  do đó ∆BCN = ∆CBM vì:  BC là cạnh chung CN = BM (gt)  (cmt) =>   =>  ∆ABC  cân tại A 

định lí đảo mà bạn

ờ thì mik viết là định lí đảo mà

sach toán 7 tập 2 bạn ơi

định lí đảo của định lí trên là: trong 1 tam giác cân thì 2 đường trung tuyến nối từ 2 đỉnh ở đáy bằng nhau

giả sử ta có tam giác ABC cân tại A, BD là đường trung tuyến nối từ đỉnh B tới AC( D thuộc AC); CE là đường trung tuyến nối từ đỉnh C tới AB( E thuộc AB) 

suy ra  B=C và

AC=AB suy ra 1/2 AB=1/2AC suy ra EA=EB=DE=DC

xét tam giác DBC và tam giác ECB có:

EB=DC(cmt)

BC(chung)
B=C(tam giác ABC cân tại A)

suy ra tam giac sDBC=ACB(c.g.c)

suy ra EC=BD

cho mk 1 tk di !!

Giả sử ∆ABC có hai đường trung tuyến BM và CN gặp nhau ở G

=> G là trọng tâm của tam giác

=> GB = BM; GC = CN

mà BM = CN (giả thiết) nên GB = GC

=> ∆GBC cân tại G => $\widehat{GCB}=\widehat{GBC}$

do đó ∆BCN = ∆CBM vì:

BC là cạnh chung

CN = BM (gt)

$\widehat{GCB}=\widehat{GBC}$ (cmt)

=> $\widehat{NBC}=\widehat{MCB}$ => ∆ABC cân tại A

giả sử tam giác ABC có 2 đường trung tuyến BM và CN gặp nhau ở G

=> G là trong tâm của tam giác

-> GB=BM ; GC = CN

mà BM=CN (gt) nên GB = GC

=> tam giác GBC cân tại G

Do đó tam giác BCN=tam giác CBM vì:

BC là cạnh chung

CN = BM (gt)

=> tam giác ABC cân tại A

xét tam giác ABD và ACE :

E=D (=90^o)

CE=BD (gt)

A:chung 

suy ra tam giác ABD =ACE(ch_gn) 

suy ra góc B=C(t/ư)

xét tam giác EIB&DIC:

E=D(=90^o)

IE=ID

B=C

suy ra tam giácEIB=DIC

suy ra IB=IC

suy ra tam giác BIC cân tại I, suy ra B=C

suy ra:đpcm