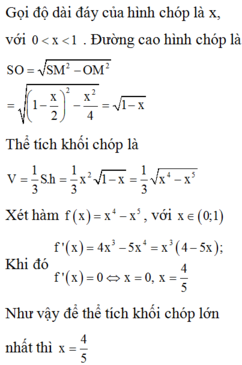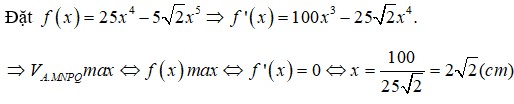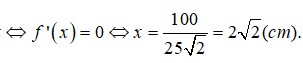Một tứ giác đều có cạnh 4cm.Diện tích của nó bằng:

Những câu hỏi liên quan
Người ta cắt một tờ giấy hình vuông có cạnh bằng
2
để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất.
Đọc tiếp
Người ta cắt một tờ giấy hình vuông có cạnh bằng 2 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất.
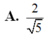
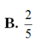
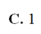
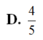
Người ta cắt một tờ giấy hình vuông có cạnh bằng
2
để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất. A.
2
5
B.
2
5
C. 1 D.
4
5
Đọc tiếp
Người ta cắt một tờ giấy hình vuông có cạnh bằng 2 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp. Tính cạnh đáy của khối chóp để thể tích của nó lớn nhất.
A. 2 5
B. 2 5
C. 1
D. 4 5
Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều (như hình vẽ). Gọi
V
1
;
V
2
lần lượt là thể tích của lăng trụ tứ giác đều và lăng trụ tam giác đều. So sánh
V...
Đọc tiếp
Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều (như hình vẽ). Gọi V 1 ; V 2 lần lượt là thể tích của lăng trụ tứ giác đều và lăng trụ tam giác đều. So sánh V 1 và V 2
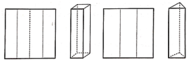
A. V 1 > V 2
B. V 1 = V 2
C. V 1 < V 2
D. Không so sánh được
Ta có V 1 = a 3 16 và V 2 = a . 1 2 . a 3 . 3 2 . a 3 = a 3 3 36 .
Do đó V 1 > V 2
Đáp án A
Đúng 0
Bình luận (0)
Kim tự tháp Ai Cập cổ đại là một trong những kỳ quan kiến trúc của thế giới. Nó có hình dạng là một khối chóp tứ giác đều. Tích diện tích hình vuông đáy với bình phương chiều cao của hình chóp bằng tổng diện tích các hình tam giác cạnh. Vậy tỷ lệ chiều cao của tam giác cạnh với chiều dài của đáy là bao nhiêu?
Thể tích của một khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng
a
3
là
Đọc tiếp
Thể tích của một khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng a 3 là
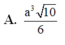
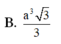
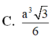
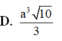
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5dm, người ta cắt bỏ bốn tam giác bằng nhau là
A
M
B
,
B
N
C
,
C
P
D
và DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất? A.
3
2
2
d...
Đọc tiếp
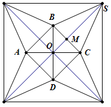
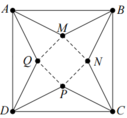
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5dm, người ta cắt bỏ bốn tam giác bằng nhau là A M B , B N C , C P D và DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
Đáp án C
Giả sử M N = x ⇒ d A ; M Q = 5 2 − x 2 0 < x < 5 2
Chiều cao hình chóp là h = 5 2 − x 2 2 − x 2 2 = 50 − 10 x 2 4
Ta có V = 1 3 M N 2 . h = 1 3 x 2 50 − 10 x 2 4 = 1 6 50 x 4 − 10 x 5 2
Đặt
f x = 50 x 4 − 10 x 5 2 ⇒ f ' x = 2 − − x 3 − 50 x 3 2 = 0 ⇒ x = 2 2 d m
Lập bảng BTT suy ra V m a x = 2 2 d m
Đúng 0
Bình luận (0)
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất A.
3
2
2
d
m
B.
5
...
Đọc tiếp
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất
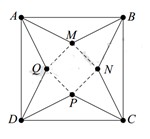
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất A.
3
2
2
d
m
B.
5
2
d
m
C.
2...
Đọc tiếp
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD, DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất
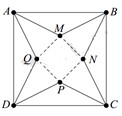
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD và DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất? A.
3
2
2
d
m
B.
5
2
d
m
C...
Đọc tiếp
Từ một tấm bìa hình vuông ABCD có cạnh bằng 5 dm, người ta cắt bỏ bốn tam giác bằng nhau là AMB, BNC, CPD và DQA. Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiêu để thể tích của nó là lớn nhất?
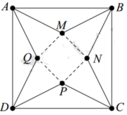
A. 3 2 2 d m
B. 5 2 d m
C. 2 2 d m
D. 5 2 2 d m