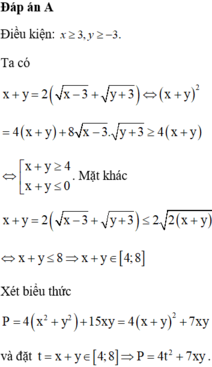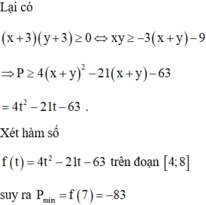C3 : Ta có ; \(B=\sqrt{x-4}+\sqrt{y-3}\) . Nhận xét : \(B\ge0\)

\(\Rightarrow B^2\le16\Rightarrow B\le4\). Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x\ge4,y\ge3\\\sqrt{x-4}=\sqrt{y-3}\\x+y=15\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=8\\y=7\end{cases}}\)

Vậy B đạt giá trị lớn nhất bằng 4 tại (x;y) = (8;7)

Tìm GTNN và mấy bài tới để từ từ mình làm cho nhé , tại mạng đang chậm...

C4 : Bạn cần thêm điều kiện x là số dương nhé : )

Ta có ; \(A=\frac{2x^2-6x+5}{2x}=x+\frac{5}{2x}-3\). Áp dụng bất đẳng thức Cauchy : 

\(x+\frac{5}{2x}\ge2\sqrt{x.\frac{5}{2x}}=\sqrt{10}\). Dấu "=" xảy ra \(\Leftrightarrow x=\frac{5}{2x}\Leftrightarrow\sqrt{\frac{5}{2}}\)

Vậy Min A = \(\sqrt{10}-3\Leftrightarrow x=\sqrt{\frac{5}{2}}\)

C5 : Bạn cần thêm điều kiện a,b là hằng số nhé :) 

\(P=\frac{\left(x+a\right)\left(x+b\right)}{x}=\frac{x^2+ax+bx+ab}{x}=x+\frac{ab}{x}+a+b\)

Áp dụng bất đẳng thức Cauchy : \(x+\frac{ab}{x}\ge2\sqrt{x.\frac{ab}{x}}=2\sqrt{ab}\Rightarrow P\ge a+2\sqrt{ab}+b=\left(\sqrt{a}+\sqrt{b}\right)^2\)

Dấu "=" xảy ra khi và chỉ khi \(x^2=ab\Leftrightarrow x=ab\) (vì a,b,x > 0)

Vậy .......

a, Từ x+y=1

=>x=1-y

Ta có: \(x^3+y^3=\left(1-y\right)^3+y^3=1-3y+3y^2-y^3+y^3\)

\(=3y^2-3y+1=3\left(y^2-y+\frac{1}{3}\right)=3\left(y^2-2.y.\frac{1}{2}+\frac{1}{4}+\frac{1}{12}\right)\)

\(=3\left[\left(y-\frac{1}{2}\right)^2+\frac{1}{12}\right]=3\left(y-\frac{1}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}\) với mọi y

=>GTNN của x³+y³ là 1/4

Dấu "=" xảy ra \(< =>\left(y-\frac{1}{2}\right)^2=0< =>y=\frac{1}{2}< =>x=y=\frac{1}{2}\) (vì x=1-y)

Vậy .......................................

b) Ta có: \(P=\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{y+x}\)

\(=\left(\frac{x^2}{y+z}+x\right)+\left(\frac{y^2}{z+x}+y\right)+\left(\frac{z^2}{y+z}+z\right)-\left(x+y+z\right)\)

\(=\frac{x\left(x+y+z\right)}{y+z}+\frac{y\left(x+y+z\right)}{z+x}+\frac{z\left(x+y+z\right)}{y+z}-\left(x+y+z\right)\)

\(=\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}-1\right)\)

Đặt \(A=\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}\)

\(A=\left(\frac{x}{y+z}+1\right)+\left(\frac{y}{z+x}+1\right)+\left(\frac{z}{y+x}+1\right)-3\)

\(=\frac{x+y+z}{y+z}+\frac{x+y+z}{z+x}+\frac{x+y+z}{y+x}-3\)

\(=\left(x+y+z\right)\left(\frac{1}{y+x}+\frac{1}{y+z}+\frac{1}{z+x}\right)-3\)

\(=\frac{1}{2}\left[\left(x+y\right)+\left(y+z\right)+\left(z+x\right)\right]\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)-3\ge\frac{9}{2}-3=\frac{3}{2}\)

(phần này nhân phá ngoặc rồi dùng biến đổi tương đương)

\(=>P=\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{y+x}-1\right)\ge2\left(\frac{3}{2}-1\right)=1\)

=>minP=1

Dấu "=" xảy ra <=>x=y=z

Vậy.....................

P=5x+3y+12/x+16/y 
=3x+12/x+y+16/y+2(x+y) 
áp dụng cosi: 3x+12/x>=2√(3.12)=12 
y+16/y>=8 
lại có 2(x+y)>=2.6=12 
nên 
P>=12+8+12=32 
dấu = khi 3x=12/x và y=16/y và x+y=6 
==> x=2; y=4 
giá trị nhỏ nhất P=32 khi x=2; y=4

làm bừa thui,ai tích mình mình tích lại

số dư lớn nhất bé hơn 175 là 174

số nhỏ nhất có 4 chữ số là 1000

Mà 1000:175=5( dư 125)

số đó là:

cho x>0, y>0 và x+y lớn hơn hoặc bằng 6.

P=5x+3y+12/x+16/y 

=3x+12/x+y+16/y+2(x+y) 

áp dụng cosi: 3x+12/x>=2√(3.12)=12 

y+16/y>=8 

lại có 2(x+y)>=2.6=12 

nên 

P>=12+8+12=32 

dấu = khi 3x=12/x và y=16/y và x+y=6 

==> x=2; y=4 

giá trị nhỏ nhất P=32 khi x=2; y=4

Ta có: x⁴ \(\ge\)0 \(\forall\)x

=> x⁴ + 5 \(\ge\)5 \(\forall\)x

=> (x⁴ + 5)² \(\ge\)25 \(\forall\)x

Dấu "=" xảy ra <=> x = 0

Vậy Min của A = 25 tại x = 0

\(A=\left(x^4+5\right)^2=x^8+10x^4+25=x^4\left(x^4+10\right)+25\)

Vì \(x^4\ge0\)và \(x^4+10>0\)

\(\Rightarrow B_{min}=25\Leftrightarrow x^4\left(x^4+10\right)=0\)

\(\Rightarrow\hept{\begin{cases}x^4=0\\x^4+10=0\end{cases}\Rightarrow\hept{\begin{cases}x=0\\x\in\varnothing\end{cases}}}\)

\(KL:B_{min}=25\Leftrightarrow x=0\)