cho tam giác ABC, có góc A =90 độ, AB =5cm, BC=13cm ;ba đường trung tuyến AM,BN ,CE giao tại D
Câu a: tính MA? BN? CE?
Câu b: diện tích tam giác bdc
Cho tam giác ABC có góc A=90 độ , AC=5cm , BC=13cm .Gọi I là trung điểm của cạnh AB,D là điểm đối xứng với C qua I
a, Tứ giác ABCD là hình gì ? Vì sao ?
b, Tính số đo diện tích tam giác ABC ?
Cho tam giác ABC có góc A=90 độ,AC=5cm,BC=13cm. I là trung điểm của AB,D đối xứng với C qua I.
a.tứ giác ADBClà hình gì?
b.M là trung điểm của BC.chứng minh MI vuông góc với AB
c.tính diện tích tam giác ABC
Câu a) Tứ giác là hình bình hành bởi vì 2 đường chéo cắt nhau tại trung điểm mỗi đường
Câu b) MI vuông góc với AB bởi vì trong tam giác ABC: MI là đường trung bình mà AC vuông góc AB suy ra MI vuông góc AB
Câu c) Áp dụng định lý Pytago thì bạn sẽ tính được cạnh AB và sẽ tính được diện tích ABC bằng 30
cho tam giác ABC , góc A bằng 90 độ, AB = 5cm, BC=13cm. Vẽ đường trung tuyến AM. gọi I là trung điểm của AM, tia BI cắt AC tại D. Tính BI
Cho tam giác ABC, góc A = 90 độ, AB = 5cm, BC = 13cm, kẻ trung tuyến AM, I là trung điểm của AM, BI cắt AC tại D. Hỏi BI bằng bao nhiêu cm?
Gọi E là trung điểm của CD.
Xét tam giác BDC ta có:
M là trung điểm của BC ( gt )
E là trung điểm của CD (cách vẽ)
=> EM là đường trung trực của tam giác BDC.
=> EM // BD => EM // ID ( I thuộc BD )
Xét tam giác AME có:
I là trung điểm của AM (gt)
EM // ID (cmt)
=> D là trung điểm của AE
Xét tam giác AME có:
I là trung điểm của AM (gt)
D là trung điểm của AE (cmt)
=> ID là đường trung bình của tam giác AME.
\(\Rightarrow ID=\frac{1}{2}ME\)
Mà \(ME=\frac{1}{2}BD\) ( ME là đường trung bình của tam giác BDC )
Nên \(ID=\frac{1}{4}BD\left(1\right)\)
Xét tam giác ABC vuông tại A ta có:
BC2 = AB2+AC2 ( Định lý Pitago thuận)
Thay:
132 = 52 + AC2
169 = 25 + AC2 => AC2 = 169 - 25 = 144
=> AC2 = 122
=> AC = 12 (cm)
Ta có: AD = ED ( D là trung điểm của AE )
ED = EC ( E là trung điểm của DC)
=> AD = ED = EC
Mà AD + ED + EC = AC (gt)
Nên: AD + AD + AD = AC
=> 3AD = AC
=> AD = AC/3
Mặt khác AC = 12 cm (cmt)
=> AD = 12/3 = 4 (cm)
Xét tam giác ABD vuông tại A ta có:
BD2 = AB2+AD2 ( định lý Pitago thuận)
BD2 = 52+42
BD2 = 25 + 20
BD2 = 45
=> \(BD=\sqrt{45}\Rightarrow BD=3\sqrt{5}\left(cm\right)\left(2\right)\)
Thế (2) vào (1) ta được:
\(ID=\frac{3\sqrt{5}}{4}\left(cm\right)\left(3\right)\)
Ta có:
BI + ID = BD ( I thuộc BD )
=> BI = BD - ID (4)
Thế (2), (3) vào (4) ta được:
\(BI=3\sqrt{5}-\frac{3\sqrt{5}}{4}\)
\(BI=3\sqrt{5}\left(1-\frac{1}{4}\right)\)
\(BI=3\sqrt{5}.\frac{3}{4}\)
\(BI=\frac{9\sqrt{5}}{4}\left(cm\right)\)
Cho tam giác ABC (A=90°) cho AB=5cm; BC=13cm
a) Tính cạnh AC , tính chu vi , diện tích tam giác ABC
b) Kẻ BD là tia phân giác góc ABC. Cạnh AB lấy điểm M sao cho BM=BA.
Chứng minh tam giác ABD=tam giác MBD từ đó suy ra DM vuông góc BC.
c) Gọi H là giao điểm của AB và BM chứng minh tam giác HBC cân
Cho tam giác ABC vuông tại A có AB = 5cm BC = 13cm kẻ AH vuông góc với BC tại H. Tính độ dài AH, CH, BH, AC.
Lời giải:
Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{13^2-5^2}=12$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{5.12}{13}=\frac{60}{13}$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{12^2-(\frac{60}{13})^2}=\frac{144}{13}$ (cm)
$BH=BC-CH=13-\frac{144}{13}=\frac{25}{13}$ (cm)
Bài 1:
1.Cho tam giác ABC: Góc A= 70 độ, góc B= 50 độ. Hãy so sánh độ dài các cạnh của tam giác ABC.
2. Cho tam giác ABC có AB= 5cm, AC= 12cm, BC= 13cm. Tam giác ABC có dạng dặc biệt nào? Vì sao?
Bài 2:
Cho tam giác ABC cân tại A ( Góc A<90 độ); các đường cao BD; CE (D thuộc AC; E thuộc AB) cắt nhau tại H
a) Chứng minh tam giác ABD= tam giác ACE
b) Chứng minh tam giác BHC là tam giác cân
b2 :
a, xét tam giác ABD và tam giác ACE có: góc A chung
AB = AC do tam giác ABC cân tại A (gt)
góc ADB = góc AEC = 90
=> tam giác ABD = tam giác ACE (ch-cgv)
b, tam giác ABD = tam giác ACE (câu a)
=> góc ABD = góc ACE (đn)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
góc HBC = góc ABC - góc ABD
góc HCB = góc ACB - góc ACE
=> góc HBC = góc HCB
=> tam giác HBC cân tại H (Dh)
còn câu 1
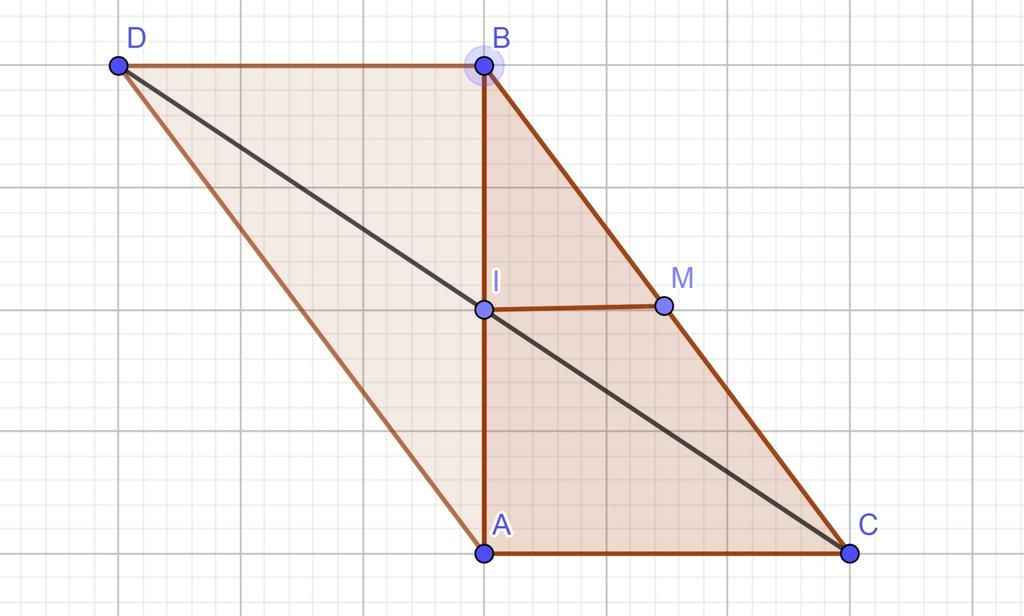
Cho tam giác ABC có A= 90 độ, AC = 5cm, BC = 13cm. Gọi I là trung điểm của cạnh AB, D là điểm đối xứng với C qua I.
a) Tứ giác ADBC là hình gì? Vì sao?
b) Gọi M là trung điểm của cạnh BC. Chứng minh: MI vuông góc với AB. Tính diện tích ΔABC.
a) Xét tứ giác \(ADBC\) ta có :
\(IB=IA\left(g.t\right)\)
\(IC=IC\) ( \(D\) đối xứng qua \(I\))
Vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Vậy tứ giác \(ADBC\) là hình bình hành
b) Xét \(\Delta ABC\) ta có :
\(IA=IB\left(g.t\right)\)
\(MB=MC\left(g.t\right)\)
\(\Rightarrow IM\) là đường trung bình \(\Delta ABC\)
Do đó : \(IM\text{/ / }AC\)
Mà \(AB\text{⊥}AC\left(A=90^o\right)\)
Vậy \(IM\text{⊥}AB\)
Áp dụng định lí pytago \(\Delta ABC\) ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)
\(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.13.5=30\left(cm^2\right)\)
Cho tam giác ABC vuông tại A, có AB = 5cm, BC = 13cm. Kẻ AH vuông góc với BC tại H. Tính độ dài các đoạn thẳng: AC, AH, BH, CH.
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=12cm\)
Ta có : \(S_{ABC}=\dfrac{1}{2}AB.AC;S_{ABC}=\dfrac{1}{2}AH.BC\Rightarrow AB.AC=AH.BC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{60}{13}cm\)
Theo định lí Pytago tam giác ABH vuông tại H
\(BH=\sqrt{AB^2-AH^2}=\dfrac{25}{13}cm\)
-> CH = BC - BH = \(13-\dfrac{25}{13}=\dfrac{154}{13}\)cm