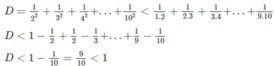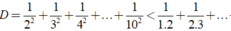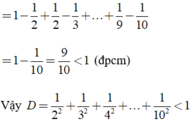122+142+...+2010
Những câu hỏi liên quan
6.
Chứng minh rằng A122+132+142+...+11021A122+132+142+...+11021
Đọc tiếp
6.
Chứng minh rằng
Chứng minh rằng với số tự nhiên n 2 thì A112+122+132+142+...+1n2�112+122+132+142+...+1�2không là số tự nhiên
Đọc tiếp
Chứng minh rằng với số tự nhiên n > 2 thì không là số tự nhiên
Chứng tỏ rằng: 1 2 2 + 1 3 2 + 1 4 2 + ... + 1 10 2 < 1
1 2 2 < 1 1.2 ; 1 3 2 < 1 2.3 ; 1 4 2 < 1 3.4 ; ... ; 1 10 2 < 1 9.10
⇒ 1 2 2 + 1 3 2 + 1 4 2 + 1 10 2 < 1 1.2 + 1 2.3 + 1 3.4 + ... + 1 9.10 < 1.
Đúng 0
Bình luận (0)
tính hợp lý:
( 102 + 112 + 122 ) : ( 132 + 142 )
(102 + 112 + 122) : (132 + 142)
= (100 + 121 + 144) :( 169 + 196)
= 365: 365
= 1
Đúng 0
Bình luận (0)
Chứng tỏ rằng: D = 1 2 2 + 1 3 2 + 1 4 2 + . . . + 1 10 2 < 1
Chứng tỏ rằng : 2 5 < 1 2 2 + 1 3 2 + 1 4 2 + 1 9 2 < 8 9
1 2 2 + 1 3 2 + 1 4 2 + ... + 1 9 2 > 1 2.3 + 1 3.4 + 1 4.5 + ... + 1 9.10 = 2 5
1 2 2 + 1 3 2 + 1 4 2 + ... + 1 9 2 < 1 1.2 + 1 2.3 + 1 3.4 + 1 8.9 = 8 9
Đúng 0
Bình luận (0)
Chứng minh rằng D = 1 2 2 + 1 3 2 + 1 4 2 + . . . + 1 10 2 < 1
Tính tổng sau
S
n
2
+
1
2
2
+
4
+
1
4
2
+
...
+
2
n...
Đọc tiếp
Tính tổng sau S n = 2 + 1 2 2 + 4 + 1 4 2 + ... + 2 n + 1 2 n 2
A. 4 n − 1 3 4 − 1 4 n + n .
B. 1 − 4 n 3 4 − 1 4 n + 2 n .
C. 4 n − 1 3 1 4 n − 4 + n .
D. 4 n − 1 3 4 − 1 4 n + 2 n .
Chọn D
S n = 2 2 + 1 2 2 + 2 + 2 4 + 1 2 4 + 2 + ... + 2 2 n + 1 2 2 n + 2 = 2 2 + 2 4 + ... + 2 2 n + 1 2 2 + 1 2 4 + ... + 1 2 2 n + 2 n = 4. 1 − 4 n 1 − 4 + 1 4 1 − 1 4 n 1 − 1 4 + 2 n = 4 n − 1 3 4 − 1 4 n + 2 n .
Đúng 0
Bình luận (0)
(102+112+122) : (132+142)
các bn giúp với ạ :(
(102 + 112 + 122) : (132 + 142)
= (100 + 121 + 144) :( 169 + 196)
= 365: 365
= 1
Đúng 2
Bình luận (0)