Gọi giao điểm AE và BP là F;

Gọi giao điểm QD và AB là H; 

Gọi kéo dài AD cắt BF tại P'     

Dễ cm M là trung điểm AC

Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)

Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\) 

\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)

Mà CM=AM (vì M là tđ AC)

\(\Rightarrow QD=DH\)

Dễ cm P là trung điểm BF

Xét \(\Delta ABP'\) có DH//BP'

\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)

Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)

\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)

Mà DH=QD (cmt) 

\(\Rightarrow BP'=FP'\)

\(\Rightarrow\)P' là trung điểm BF

\(\Rightarrow P\equiv P'\)

\(\Rightarrow A,D,P\) thẳng hàng

Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:

\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)

Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:

\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)

M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'

\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)

Gọi \(d_1\) là ảnh của d qua phép đối xứng trục

Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:

\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)

Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d

Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:

\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)

Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:

\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)

B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'

\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)

\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)

\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt

Phương trình \(d_1\):

\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)

a: Xét ΔABD và ΔEBD có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔABD=ΔEBD

Suy ra: DE⊥BC

?

a) Xét ΔMNI vuông tại M và ΔHPI vuông tại P có

\(\widehat{MIN}=\widehat{HIP}\)(hai góc đối đỉnh)

Do đó: ΔMNI\(\sim\)ΔHPI(g-g)

b) Ta có: ΔMNI\(\sim\)ΔHPI(cmt)

nên \(\widehat{MNI}=\widehat{HPI}\)(hai góc tương ứng)

hay \(\widehat{MNI}=\widehat{MPK}\)

Xét ΔMNI vuông tại M và ΔMPK vuông tại M có

\(\widehat{MNI}=\widehat{MPK}\)(cmt)

Do đó: ΔMNI\(\sim\)ΔMPK(g-g)

Suy ra: \(\dfrac{MN}{MP}=\dfrac{MI}{MK}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)

Xét ΔMNP vuông tại M và ΔMIK vuông tại M có

\(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)(cmt)

Do đó: ΔMNP\(\sim\)ΔMIK(c-g-c)

\(a,ĐK:x\ge0;x\ne9\\ A=\dfrac{x+3\sqrt{x}-\sqrt{x}+3-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{x+2\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\)

\(b,x=\sqrt{14-6\sqrt{5}}+\sqrt{6+2\sqrt{5}}=\sqrt{\left(3-\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}+1\right)^2}\\ =3-\sqrt{5}+\sqrt{5}+1=4\\ \Leftrightarrow A=\dfrac{2-1}{2-3}=\dfrac{1}{-1}=-1\)

a: \(\widehat{C}=30^0\)

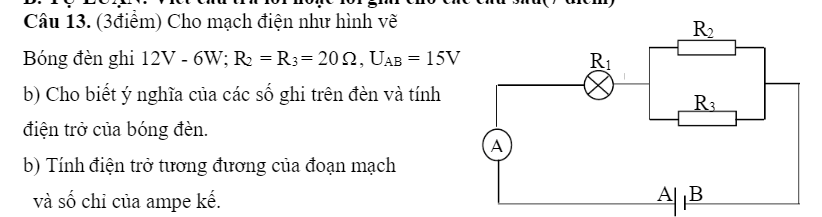
Điện trở đèn:

\(R=\dfrac{U^2}{P}=\dfrac{12^2}{6}=24\Omega\)

Hai điện trở \(R_2;R_3\) mắc song song nhau\(\Rightarrow R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{20\cdot20}{20+20}=10\Omega\)

Điện trở tương đương:

\(R=R_Đ+R_{23}=24+10=34\Omega\)

Dòng điện qua mạch lúc này: \(I=\dfrac{U}{R}=\dfrac{15}{34}=0,44A\)

b, Điển trở R₁ của bóng đèn:

Từ công thức: \(P=\dfrac{U^2}{R}\Rightarrow R_1+\dfrac{U^2}{P}=12^2:6=24\Omega\)

Điện trở tương đương của đoạn mạch:

Vì R₁ nt \(\left(R_2//R_3\right)\) nên \(R_{tđ}=R_1+\dfrac{R_2.R_3}{R_2+R_3}=24+\dfrac{20.20}{20+20}=34\Omega\)

Số chỉ của ampe kế: \(I=\dfrac{U}{R}=15:34=0,44A\)

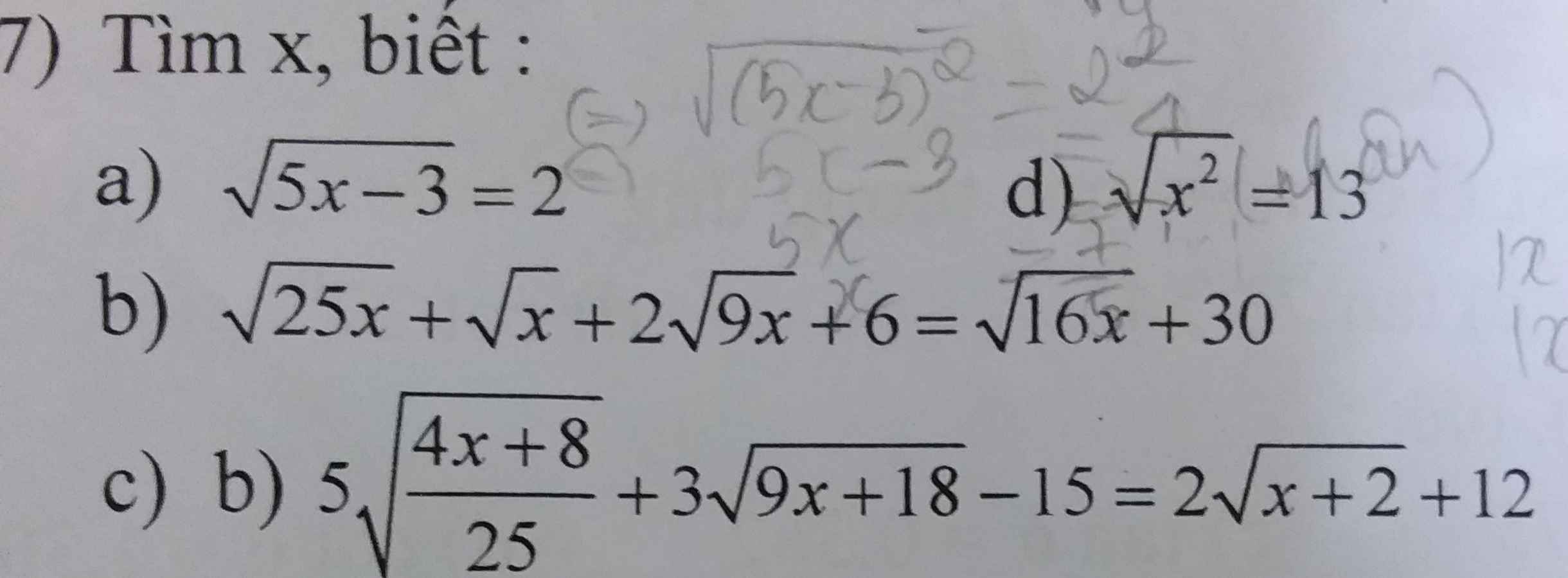
\(a,\Leftrightarrow5x-3=4\Leftrightarrow x=\dfrac{12}{5}\\ b,ĐK:x\ge0\\ PT\Leftrightarrow5\sqrt{x}+\sqrt{x}+6\sqrt{x}+6=4\sqrt{x}+30\\ \Leftrightarrow8\sqrt{x}=24\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ c,ĐK:x\ge-2\\ PT\Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-15=2\sqrt{x+2}+12\\ \Leftrightarrow9\sqrt{x+2}=27\\ \Leftrightarrow\sqrt{x+2}=3\\ \Leftrightarrow x+2=9\\ \Leftrightarrow x=7\left(tm\right)\\ d,\Leftrightarrow\left|x\right|=13\Leftrightarrow\left[{}\begin{matrix}x=13\\x=-13\end{matrix}\right.\)

a: \(\Leftrightarrow5x-3=4\)

hay \(x=\dfrac{7}{5}\)

b) ĐKXĐ: \(x\ge0\)

\(pt\Leftrightarrow5\sqrt{x}+\sqrt{x}+6\sqrt{x}-4\sqrt{x}=30-6\)

\(\Leftrightarrow8\sqrt{x}=24\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\)

c) ĐKXĐ: \(x\ge-2\)

\(pt\Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-2\sqrt{x+2}=12+15\)

\(\Leftrightarrow9\sqrt{x+2}=27\Leftrightarrow\sqrt{x+2}=3\)

\(\Leftrightarrow x+2=9\Leftrightarrow x=7\left(tm\right)\)