Tìm các số ngyên x,y biết:
(2x + 5y + 1)(2|x| + y + x2 +x) =105
tìm số ngyên x,y biết: 3xy - 2x + 5y = 9
Lời giải:
$3xy-2x+5y=9$
$x(3y-2)+5y=9$
$3x(3y-2)+15y=27$
$3x(3y-2)+5(3y-2)=17$
$(3x+5)(3y-2)=17$
Do $x,y$ nguyên nên $3x+5, 3y-2$ cũng là số nguyên. Ta có bảng sau: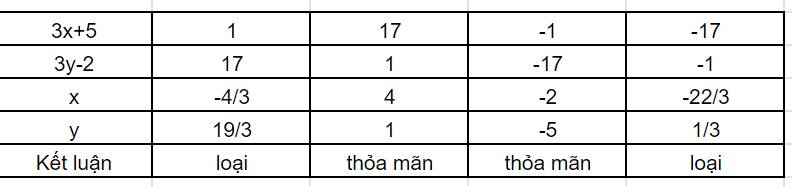
Tìm nghiệm nguyên dương của phương trình sau:
(2x + 5y + 1)(2|x| + y + x2 + x) = 105
Do VP là số lẻ
<=> 2x + 5y + 1 là số lẻ và \(2^{\left|x\right|}+y+x^2+x\) là số lẻ
<=> y chẵn và \(2^{\left|x\right|}+y+x\left(x+1\right)\) là số lẻ
=> \(2^{\left|x\right|}\) là số lẻ (do y chẵn và x(x+1) chẵn)
=> x = 0
PT <=> \(\left(5y+1\right)\left(1+y\right)=105\)
<=> y = 4 (thử lại -> thỏa mãn)
KL: x = 0; y = 4
Tìm x,y là số nguyên tố biết
(2x+5y+1)(2x+y+x2+x)=105
tìm các số nguyên x,y thỏa mãn (2x+5y+1)(2^|x|+y+x^2+x=105 chỉ có 2^|x| thui ná.
đậu xanh đậu đỏ
đậu đen đậu vàng
bạn ơi cùng đậu
xem vui không nào...
tìm 3 số x,y,z thỏa mãn (2x + 5y + 1).(2^|x| +y + x^2 +x)=105
Tham khảo câu hỏi của White Boy nhé ~"Huy"
Giải phương trình nghiệm nguyên 2x+5y+1)(2|x|+y+x+x2)=105
Tìm x,y,z là số nguyên thoả mãn: (2x+5y+1)(2|x|+y+x2+x)=105
1. Tìm a,b ∈ Z+(a,b ≠1) để 2a+3b là số chính phương
2. Tìm nghiệm nguyên không âm của phương trình:
\(\left(2x+5y+1\right)\left(2020^{\left|x\right|}+y+x^2+x\right)=105\)
3. Tìm x,y,z ∈ Z+ t/m:
\(xy+y-x!=1;yz+z-y!=1;x^2-2y^2+2x-4y=2\)
4. Tìm tất cả các số nguyên tố p;q;r sao cho:
pq+qp=r
5. Tìm nghiệm nguyên tố của phương trình:
\(x^y+y^x+2022=z\)
6. CMR: Với n ∈ N và n>2 thì 2n-1 và 2n+1 không thể đồng thời là 2 số chính phương
Bài 2: Ta có:
\(\left(2x+5y+1\right)\left(2020^{\left|x\right|}+y+x^2+x\right)=105\) là số lẻ
\(\Rightarrow\left\{{}\begin{matrix}2x+5y+1\\2020^{\left|x\right|}+y+x^2+x\end{matrix}\right.\) đều lẻ
\(\Rightarrow y⋮2\)\(\Rightarrow2020^{\left|x\right|}⋮̸2\Leftrightarrow\left|x\right|=0\Leftrightarrow x=0\).
Thay vào tìm được y...
Lúc nãy bận thi online nên giờ mới làm tiếp được, bạn thông cảm.
Bài 4:
Do p; q; r là các SNT nên \(p^q+q^p>2^2+2^2=8\Rightarrow r>8\) nên r là SNT lẻ
Mà r lẻ thì trong 2 số \(p^q;q^p\) phải có 1 số lẻ, một số chẵn.
Do vai trò p; q như nhau nên không mất tính tổng quát ta giả sử p lẻ, q chẵn
\(\Rightarrow q=2\). Lúc này ta có:
\(p^2+2^p=r\)
+Xét p=3\(\Rightarrow p^2+2^p=r=17\left(tm\right)\) (Do p lẻ nên loại TH p=2)
+Xét p>3. Ta có:
\(\left\{{}\begin{matrix}p^2\equiv1\left(mod3\right)\\2^p\equiv\left(-1\right)^p\equiv-1\left(mod3\right)\end{matrix}\right.\)
\(\Rightarrow p^2+2^p\equiv1+\left(-1\right)\equiv0\left(mod3\right)\)
\(\Rightarrow\left(p^2+2^p\right)⋮3\) mà \(p^2+2^p>3\) nên là hợp số
\(\Rightarrow r\) là hợp số, không phải SNT, loại.
Vậy ta có \(\left(p;q;r\right)\in\left\{\left(3;2;17\right);\left(2;3;17\right)\right\}\) tm đề bài
Bài 6: Ta có 1SCP lẻ chia cho 4 dư 1.
Nếu 2n-1 là SCP thì ta có
\(2n-1\equiv1\left(mod4\right)\Leftrightarrow2n+1\equiv3\left(mod4\right)\)
Do đó 2n+1 không là SCP
\(\Rightarrowđpcm\)
Tìm cặp số tự nhiên thỏa mãn (2x+5y+1)(2x+y+2x)=105