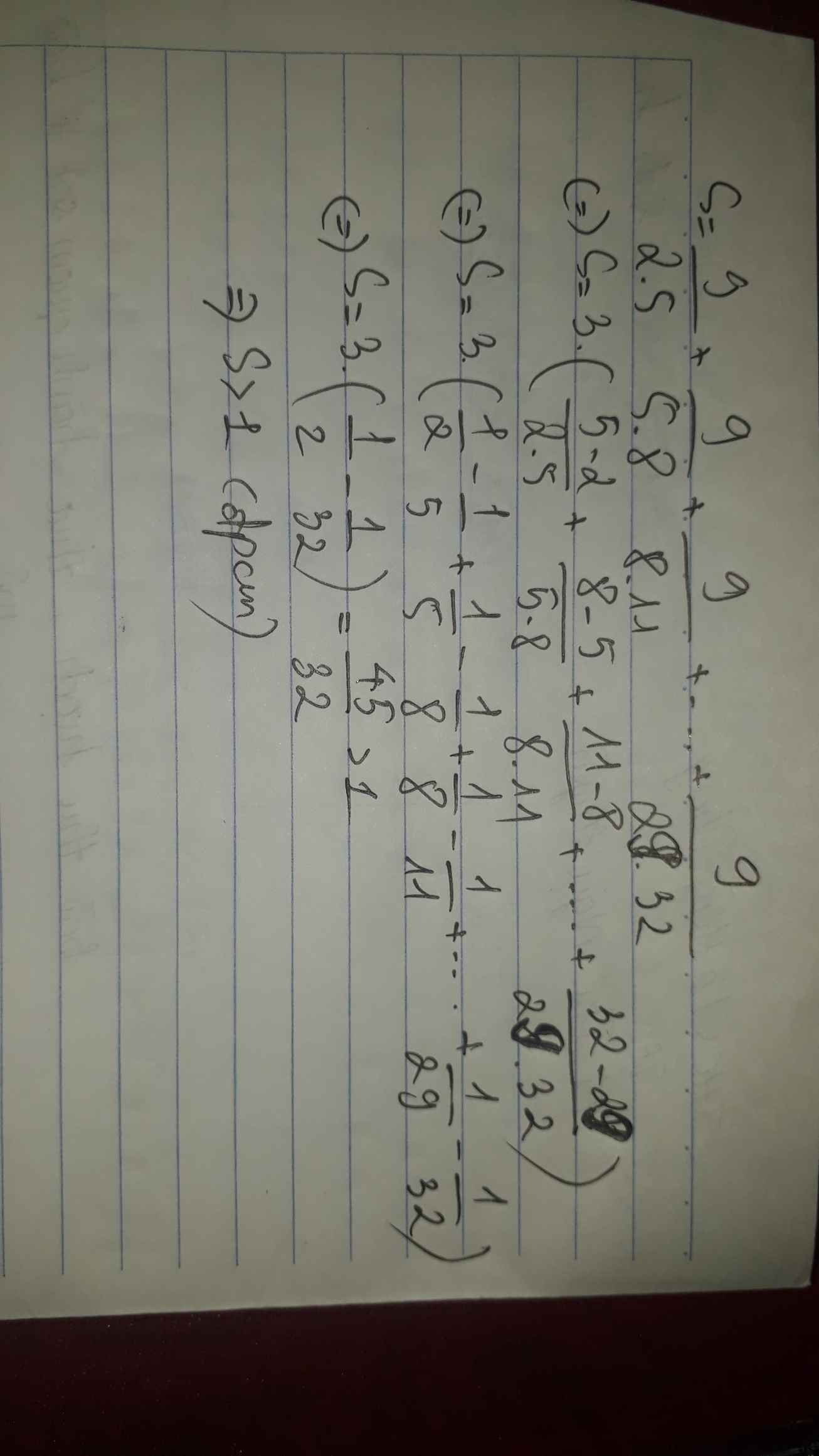\(S=2.\left(\frac{3}{2.5}+\frac{3}{5.8}+...+\frac{3}{29.32}\right)\)

\(S=2.\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+...+\frac{1}{29}-\frac{1}{32}\right)\)

\(S=2.\left(\frac{1}{2}-\frac{1}{32}\right)\)

\(S=1-\frac{1}{16}< 1\)

Vậy \(S< 1\)

\(\frac{12}{2.5}+\frac{12}{5.8}+\frac{12}{8.11}+...+\frac{12}{29.32}\)

\(=4.\left(\frac{3}{2.5}+\frac{3}{5.8}+\frac{3}{8.11}+...+\frac{3}{29.32}\right)\)

\(=4.\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{29}-\frac{1}{32}\right)\)

\(=4.\left(\frac{1}{2}-\frac{1}{32}\right)\)

\(=4.\frac{15}{32}\)

\(=\frac{15}{8}\)

_Chúc bạn học tốt_

\(\frac{12}{2.5}+\frac{12}{5.8}+\frac{12}{8.11}+....+\frac{12}{29.32}\)

\(=4\left(\frac{3}{2.5}+\frac{3}{5.8}+\frac{3}{8.11}+...+\frac{3}{29.32}\right)\)

\(=4\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+...+\frac{1}{29}-\frac{1}{32}\right)\)

\(=4\left(\frac{1}{2}-\frac{1}{32}\right)\)

\(=4.\frac{15}{32}=\frac{15}{8}\)

Đặt A= 12/2*5+12/5*8+12/8*11+....+12/29*32

       A= 4*(3/2*5+3/5*8+3/8*11+...+3/29*32)

       A = 4*(1/2-1/5+1/5-1/8+1/8-1/11+....+1/29-1/32)

       A= 4*(1/2-1/32)

       A= 4*15/32

       A= 15/8

\(S=\frac{6}{2.5}+\frac{6}{5.8}+\frac{6}{8.11}+...+\frac{6}{29.32}\)

\(S=2.\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{29}-\frac{1}{32}\right)\)

\(S=2.\left(\frac{1}{2}-\frac{1}{32}\right)\)

\(S=2.\frac{15}{31}\Rightarrow S=\frac{15}{16}< 1\)

\(S=\frac{6}{2.5}+\frac{6}{5.8}+\frac{6}{8.11}+...+\frac{6}{29.32}\)  

\(S=\left(\frac{1}{2}-\frac{1}{5}\right)+\left(\frac{1}{5}-\frac{1}{8}\right)+\left(\frac{1}{8}-\frac{1}{11}\right)+...+\left(\frac{1}{29}-\frac{1}{32}\right)\)

\(S=\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{29}-\frac{1}{32}\)

\(S=\frac{1}{2}-\frac{1}{32}\)

\(S=\frac{17}{32}< 1\)

S=6/2.5+6/5.8+6/8.11+...+6/29.32
S=2.(1/2-1/5+1/5-1/8+1/8-1/11+...+1/29-1/32)
S=2.(1/2+1/32)
S=2.15/32
S=30/32=15/16
=>S<1

\(S=\frac{6}{2.5}+\frac{6}{5.8}+.......+\frac{6}{29.32}\)

\(S=2\left(\frac{3}{2.5}+\frac{3}{5.8}+......+\frac{3}{29.32}\right)\)

\(S=2\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+......+\frac{1}{29}-\frac{1}{32}\right)\)

\(S=2\left(\frac{1}{2}-\frac{1}{32}\right)\)

\(S=2.\frac{15}{32}\)

\(S=\frac{15}{16}< 1\RightarrowĐPCM\)

Vậy \(S=\frac{15}{16}\)

Bài 1 :

S = \(\frac{6}{2.5}+\frac{6}{5.8}+...+\frac{6}{29.32}\)

   = 2 . \(\left(\frac{3}{2.5}+\frac{3}{5.8}+...+\frac{3}{29.32}\right)\)

   = 2 . \(\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+...+\frac{1}{29}-\frac{1}{32}\right)\)

   = 2 . \(\left(\frac{1}{2}-\frac{1}{32}\right)\)= ....

cả 2 cái cộng lại hay là từng cái một vậy bạn?

a) Ý bạn là: \(S_1=\frac{3}{4}+\frac{3}{4\cdot7}+\frac{3}{7\cdot10}+...+\frac{3}{40\cdot43}\)đúng không?

\(S_1=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{40}-\frac{1}{43}\)

\(S_1=1-\frac{1}{43}< 1\left(đpcm\right)\)

b) \(S_2=\frac{6}{2\cdot5}+\frac{6}{5.8}+\frac{6}{8\cdot11}+...+\frac{6}{29\cdot32}\)

=>\(\frac{S_2}{2}=\frac{3}{2\cdot5}+\frac{3}{5.8}+\frac{3}{8\cdot11}+...+\frac{3}{29\cdot32}\)

\(\frac{S_2}{2}=\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{29}-\frac{1}{32}\)

\(\frac{S_2}{2}=\frac{1}{2}-\frac{1}{32}=\frac{16}{32}-\frac{1}{32}=\frac{15}{32}\)

=>\(S_2=\frac{15}{32}\cdot2=\frac{15}{16}< 1\left(đpcm\right)\)

= 1/2 - 1/5 + 1/5 - 1/8 + 1/8 - 1/11 + .... + 1/29 - 1/32

= 1/2 - 1/32

= ..... ( tự bấm máy tính nhé )

Ta có: \(E=\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+....+\frac{1}{29}-\frac{1}{32}\)

     \(\Rightarrow E=\frac{1}{2}-\frac{1}{32}\)

     \(\Rightarrow E=\frac{16-1}{32}=\frac{15}{32}\)

 Vậy \(E=\frac{15}{32}\)

E=5-2/2×5 + 8-5/5×8+11-8/8×11+.....+32-29/29×32

E=1/2-1/5+1/5-1/8+1/8-1/11+......+1/29-1/32

E=1/2-1/32

E=15/32

Ta có: 9/2.5  + 9/5.8 + 9/9.11+...+ 9/29.32

      =>9.(1/2 -1/5 + 1/5 - 1/8 +...+1/29 -1/32)

      =>9.( 1/2 -1/32)

      =>9. 15/32

      =>45/32 

Suy ra 45/32 >1 nên S>1

Ta có: \(S=\dfrac{9}{2\cdot5}+\dfrac{9}{5\cdot8}+\dfrac{9}{8\cdot11}+...+\dfrac{9}{29\cdot32}\)

\(=3\left(\dfrac{3}{2\cdot5}+\dfrac{3}{5\cdot8}+\dfrac{3}{8\cdot11}+...+\dfrac{3}{29\cdot32}\right)\)

\(=3\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{29}-\dfrac{1}{32}\right)\)

\(=3\left(\dfrac{1}{2}-\dfrac{1}{32}\right)\)

\(=3\cdot\dfrac{15}{32}=\dfrac{45}{32}>1\)

tham khảo ở đây nha

https://olm.vn/hoi-dap/detail/222956295982.html

\(A=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{150}-\dfrac{1}{153}\right)\)

\(=\dfrac{1}{3}.\dfrac{151}{306}=\dfrac{151}{918}\)