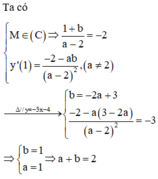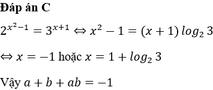Biết rằng : | a+7 |+| b-3 |=0. Khi đó tổng a + b có giá trị là

Những câu hỏi liên quan
Biết rằng
∫
e
2
x
cos
3
x
d
x
e
2
x
a
cos
3
x
+
b
sin
3
x
+
c
trong đó a, b, c là các hằng số, khi đó tổng a +...
Đọc tiếp
Biết rằng
∫
e
2
x
cos
3
x
d
x
=
e
2
x
a
cos
3
x
+
b
sin
3
x
+
c
trong đó a, b, c là các hằng số, khi đó tổng a + b có giá trị là
A. - 1 13
B. - 5 13
C. 5 13
D. 1 13
Chọn C.
Đặt f x = e 2 x a cos 3 x + b sin 3 x + c
Ta có f ' x = 2 a + 3 b e 2 x cos 3 x + 2 b - 3 a e 2 x sin 3 x
Để f(x) là một nguyên hàm của hàm số e 2 x cos 3 x , điều kiện là
f ' ( x ) = e 2 x cos 3 x ⇔ 2 a + 3 b = 1 2 b - 3 a = 0 ⇔ a = 2 13 b = 3 13 ⇒ a + b = 5 13
Đúng 0
Bình luận (0)
Biết rằng
∫
e
2
x
cos
3
xdx
e
2
x
a
cos
3
x
+
b
sin
3
x
+
c
, trong đó a, b, c là các hằng số, khi đó tổng a + b có giá trị là A.
-...
Đọc tiếp
Biết rằng ∫ e 2 x cos 3 xdx = e 2 x a cos 3 x + b sin 3 x + c , trong đó a, b, c là các hằng số, khi đó tổng a + b có giá trị là
A. - 1 13
B. - 5 13
C. 5 13
D. 1 13
Cho hàm số
y
x
+
b
a
x
−
2
có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm
M
1
;
−
2
song song với đường thẳng
3
x
+
y
−
4...
Đọc tiếp
Cho hàm số y = x + b a x − 2 có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm M 1 ; − 2 song song với đường thẳng 3 x + y − 4 = 0. Khi đó tổng giá trị của a + b bằng:
A. 2
B. 1
C. -1
D. 0
biết rằng phương trình \(x^2+px+1=0\) có nghiệm là a,b và phương trình \(x^2+qx+2=0\) có nghiêm là b,c . Khi đó giá trị của biểu thức \(A=pq-\left(b-a\right)\left(b-c\right)\)bằng ?
Áp dụng viet vào pt \(x^2+px+1=0\) ta được:\(\left\{{}\begin{matrix}a+b=-p\\ab=1\end{matrix}\right.\)
Áp dụng viet vào pt \(x^2+qx+2=0\) ta được:\(\left\{{}\begin{matrix}b+c=-q\\bc=2\end{matrix}\right.\)
\(A=pq-\left(b-a\right)\left(b-c\right)=-\left(a+b\right).-\left(b+c\right)-\left(b^2-bc-ab+ac\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
\(=2ab+2bc=6\)
Đúng 3
Bình luận (0)
Phương trình: \(x^2+px+1=0\)
Có 2 nghiệm:a,b
\(\Rightarrow\left\{{}\begin{matrix}a+b=-p\\a.b=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}p=-\left(a+b\right)\\1=a.b\end{matrix}\right.\)
Phương trình \(x^2+px+2=0\)
Có 2 nghiệm:b,c
\(\Rightarrow\left\{{}\begin{matrix}b+c=-q\\b.c=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}q=-\left(b+c\right)\\2=b.c\end{matrix}\right.\)
Ta có: \(p.q-\left(b-a\right)\left(b-c\right)\)
\(=-\left(a+b\right).\left[-\left(b+c\right)\right]-\left(b-a\right)\left(b-c\right)\)
\(=\left(a+b\right)\left(b+c\right)-\left(b-a\right)\left(b-c\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
=\(\left(ab+ab\right)+\left(ac-ac\right)+\left(b^2-b^2\right)+\left(bc+bc\right)\)
\(=2ab+2bc\)
\(=2.1+2.2\)
=6
-Chúc bạn học tốt-
Đúng 1
Bình luận (0)
Cho hàm số
y
x
3
-
3
m
x
2
+
3
m
3
. Biết rằng có hai giá trị của tham số m để đồ thị hàm số có hai điểm cực trị A, B và tam giác OAB có diện tích bằng 48 . Khi đó tổng hai giá trị của m...
Đọc tiếp
Cho hàm số y = x 3 - 3 m x 2 + 3 m 3 . Biết rằng có hai giá trị của tham số m để đồ thị hàm số có hai điểm cực trị A, B và tam giác OAB có diện tích bằng 48 . Khi đó tổng hai giá trị của m là:
A. 2
B. -2
C. 0
D. 2
Chọn: C
![]()
![]()
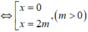
Tọa độ hai điểm cực trị: A 0 ; 3 m 3 , B 2 m ; - m 3
![]()
Ta có: y = y ' . 1 3 x - m 3 - 2 m x + 3 m 3
⇒ Phương trình đường thẳng đi qua hai điểm cực trị là:
![]()
⇒ d O ; A B = 3 m 3 4 m 4 + 1
Diện tích tam giác OAB là;
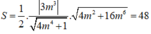
![]()
Tổng hai giá trị của m là: -2 + 2 = 0
Đúng 0
Bình luận (0)
Câu 1.8: Biết x là một số tự nhiên có hai chữ số, biết nếu đem x chia cho tổng các chữ số của x thì được thương là 4, dư là 3. Còn nếu đem x chia cho tích các chữ số của x thì được thương là 3 và dư là 5. Khi đó x ......Câu 1.9: Biết rằng phương trình x2 + px + 1 0 có 2 nghiệm là a, b và phương trình x2 + qx + 2 0 có 2 nghiệm b, c. Khi đo giá trị của biểu thức A pq - (b - a)(b - c) ...........Câu 1.10: Cho x; y 0 thỏa mãn x + y ≤ 1. Giá trị nhỏ nhất của biểu thức là: .......giúp e với!! ma...
Đọc tiếp
Câu 1.8: Biết x là một số tự nhiên có hai chữ số, biết nếu đem x chia cho tổng các chữ số của x thì được thương là 4, dư là 3. Còn nếu đem x chia cho tích các chữ số của x thì được thương là 3 và dư là 5. Khi đó x = ......
Câu 1.9: Biết rằng phương trình x2 + px + 1 = 0 có 2 nghiệm là a, b và phương trình x2 + qx + 2 = 0 có 2 nghiệm b, c. Khi đo giá trị của biểu thức A = pq - (b - a)(b - c) = ...........
Câu 1.10: Cho x; y > 0 thỏa mãn x + y ≤ 1. Giá trị nhỏ nhất của biểu thức là: .......
giúp e với!! mai e thi r!!! hụ hụ
Biết rằng phương trình
2
x
2
-
1
3
x
+
1
có 2 nghiệm là a, b. Khi đó a + b + ab có giá trị bằng A.
-
1
+
2
l
o
g
2
3
B.
1
+
l
o...
Đọc tiếp
Biết rằng phương trình 2 x 2 - 1 = 3 x + 1 có 2 nghiệm là a, b. Khi đó a + b + ab có giá trị bằng
A. - 1 + 2 l o g 2 3
B. 1 + l o g 2 3
C. -1
D. 1 + 2 l o g 2 3
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (2; -3; 7), B (0; 4; -3) và C (4; 2; 5). Biết điểm
M
x
0
;
y
0
;
z
0
nằm trên (Oxy) sao cho
M...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (2; -3; 7), B (0; 4; -3) và C (4; 2; 5). Biết điểm M x 0 ; y 0 ; z 0 nằm trên (Oxy) sao cho M A → + M B → + M C → có giá trị nhỏ nhất. Khi đó tổng P = x 0 + y 0 + z 0 bằng:
A. P = 0
B. P = 6
C. P = 3
D. P = -3
Chọn C
Gọi G là trọng tâm tam giác ABC => G = (2; 1; 3)
Khi đó ![]()
Nên ![]() có giá trị nhỏ nhất khi và chỉ khi MG ngắn nhất, khi đó M là hình chiếu vuông góc của G (2; 1; 3) trên (Oxy)
có giá trị nhỏ nhất khi và chỉ khi MG ngắn nhất, khi đó M là hình chiếu vuông góc của G (2; 1; 3) trên (Oxy)
Do đó M (2; 1; 0).
Vậy ![]()
Đúng 0
Bình luận (0)
Biết rằng nguyên hàm của \(e^{2x}cos3xdx=e^{2x}\left(acos3x+bsin3x\right)+c\) .Trong đó a,b,c là các hằng số , khi đó tổng a+b có giá trị là ? (Đáp án:\(\frac{5}{13}\))