Chứng minh AN vuông góc với BC.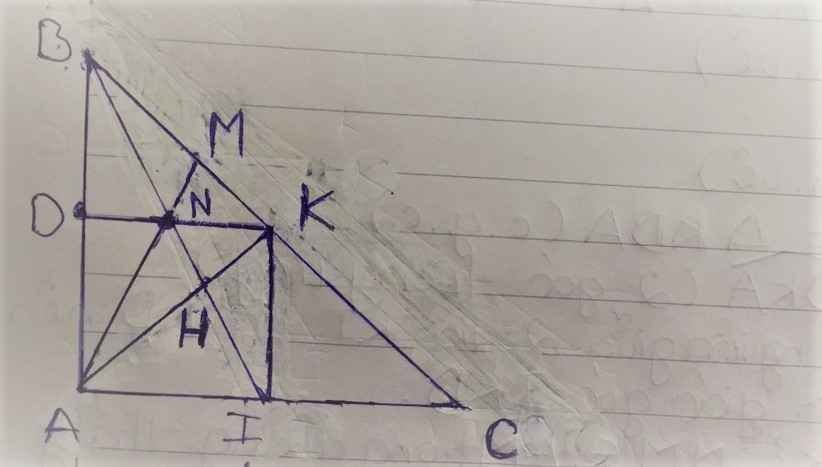

Những câu hỏi liên quan
Cho tam giác ABC, góc C bằng 70 độ, góc A bằng 40 độ. Trên tia đối của tia AC lấy điểm O. Trên nửa mặt phẳng bờ AC có chứ B, vẽ tia Ox sao cho góc xOA bằng 110 độ.a, Chứng minh: Ox // BC.b, Kẻ At là tai p/giác của góc OAB. Chứng minh: At // BC.c, Kẻ tia AN là phân giác góc ABC. Chứng minh AN vuông góc với At.d, Chứng minh: AN vuông góc với BC, AN vuông góc với Ox.(Vẽ hình giúp mình nhé)
Đọc tiếp
Cho tam giác ABC, góc C bằng 70 độ, góc A bằng 40 độ. Trên tia đối của tia AC lấy điểm O. Trên nửa mặt phẳng bờ AC có chứ B, vẽ tia Ox sao cho góc xOA bằng 110 độ.
a, Chứng minh: Ox // BC.
b, Kẻ At là tai p/giác của góc OAB. Chứng minh: At // BC.
c, Kẻ tia AN là phân giác góc ABC. Chứng minh AN vuông góc với At.
d, Chứng minh: AN vuông góc với BC, AN vuông góc với Ox.
(Vẽ hình giúp mình nhé)
.CHO TAM giác ABC vuông cân tại A.Vẽ AH vuông góc với BC
a) Chứng minh tam giác AHB=tam giác AHC
b)Vẽ HM vuông góc với AB,HN vuông góc với AC.CM AMN cân
c)Chứng minh MN//BC
d)Chứng minh AH^2+BM^2=AN^2+BH^2
cho tam giác ABC vuông cân tại A.Vẽ AH vuông góc với BC
a) Chứng minh tam giác AHB=tan giác AHC
b) VẼ HM vuông góc với AB,HN vuông góc với AC.Chứng minh tam giác AMN cân
c) Chứng minh MN//BC
d) Chứng minh AH^2+BM^2=AN^2+BH^2
tam giacs ABC cân tại A. AH vuông góc với BC. a. Chứng minh tam giác AHB bằng tam giac AHC b. HM vuông góc với AB, HN vuông góc với AC, Chứng mình tam giác AMN cân . c. MN//Bc, d. Chứng minh AH^2+BM^2=AN^2+BH^2
@trần thị giang : thì mình KHÔNG hỏi bạn, nếu ai biết thì trả lời, CÂM ĐƯỢC RỒI
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=AC. Gọi N là trung điểm của cạnh BC. a)Chứng minh tam giác ANB=tam giác ANC b)Chứng minh góc ANB =góc ANC và AN vuông góc với BC c) Kẻ ND vuông góc với AC( D thuộc AC). Tính số đo của góc AND
a: Xét ΔANB và ΔANC có
AN chung
NB=NC
AB=AC
Do đó: ΔANB=ΔANC
b: Ta có: ΔABC cân tại A
mà AN là đường trung tuyến
nên AN là đường cao
c: Ta có: ΔANC vuông cân tại N
mà ND là đường cao
nên ND là đường trung tuyến
=>ND=AD
=>ΔAND vuông cân tại D
hay \(\widehat{AND}=45^0\)
Đúng 0
Bình luận (1)
Cho tam giác ABC cân tại A. Vẽ AH vuông góc BC. a) Chứng minh tam giác AHB=tam giác AHC b) Vẽ HM vuông góc AB, HN vuông góc AC, chứng minh tam giác AMN cân c) Chứng minh MN song song với BC d) Chứng minh AH ^2 + BM^2=AN^2 +BH^2
Vẽ hộ em hình nwuax ạ
a, Xét tam giác AHB và tam giác AHC có
AH _ chung
AB = AC
Vậy tam giác AHB~ tam giác AHC (ch-cgv)
Ta có tam giác ABC cân tại A, có AH là đường cao
đồng thười là đường pg
b, Xét tam giác AMH và tam giác NAH có
HA _ chung
^MAH = ^NAH
Vậy tam giác AMH = tam giác NAH (ch-gn)
=> AM = AN ( 2 cạnh tương ứng )
c, Ta có AM/AB = AN/AC => MN // BC
d, Ta có \(AH^2+BM^2=AN^2+BH^2\)
Xét tam giác BMH vuông tại M \(MB^2=BH^2-MH^2\)
Thay vào ta được \(AH^2+BH^2-MH^2=AN^2+BH^2\Leftrightarrow AH^2-MH^2=AN^2\)
Lại có AM = AN (cmt)
\(AM^2=AH^2-MH^2\)( luôn đúng trong tam giác AMH vuông tại M)
Vậy ta có đpcm
Đúng 1
Bình luận (1)
cho tam giác ABC có ABAC M là trung điểm của BC Chứng minh AM là phân giác của góc BAC chứng minh AM vuông góc với BC chứng minh M là trung điểm của AN
Đọc tiếp
cho tam giác ABC có AB=AC M là trung điểm của BC Chứng minh AM là phân giác của góc BAC chứng minh AM vuông góc với BC chứng minh M là trung điểm của AN
Cho hình bình hành ABCD. Kẻ AM vuông góc với BC, AN vuông góc với CD.
a, Chứng minh rằng AM : AN = AB : BC.
b, Gọi I, J lần lượt là trung điểm của AB, AD. Chứng minh rằng diện tích hình ABCD = 2 lần diện tích hình AICJ.
Cho tam giác cân ABC, AB = AC. Trên tia đối của các tia BA, CA lấy 2 điểm D và E sao cho BD = CE.
a. Chứng minh DE // BC
b. Từ D kẻ DM vuông góc với BC, từ E kẻ EN vuông góc với BC. Chứng minh DM = EN
c. Chứng minh tam giác AMN cân
d. Từ B, C kẻ các đường vuông góc với AM, AN chúng cắt nhau tại I. Chứng minh AI là phân giác chung của 2 góc BAC, MAC
https://h.vn/hoi-dap/question/168197.html
tham khảo nhé bạn



















