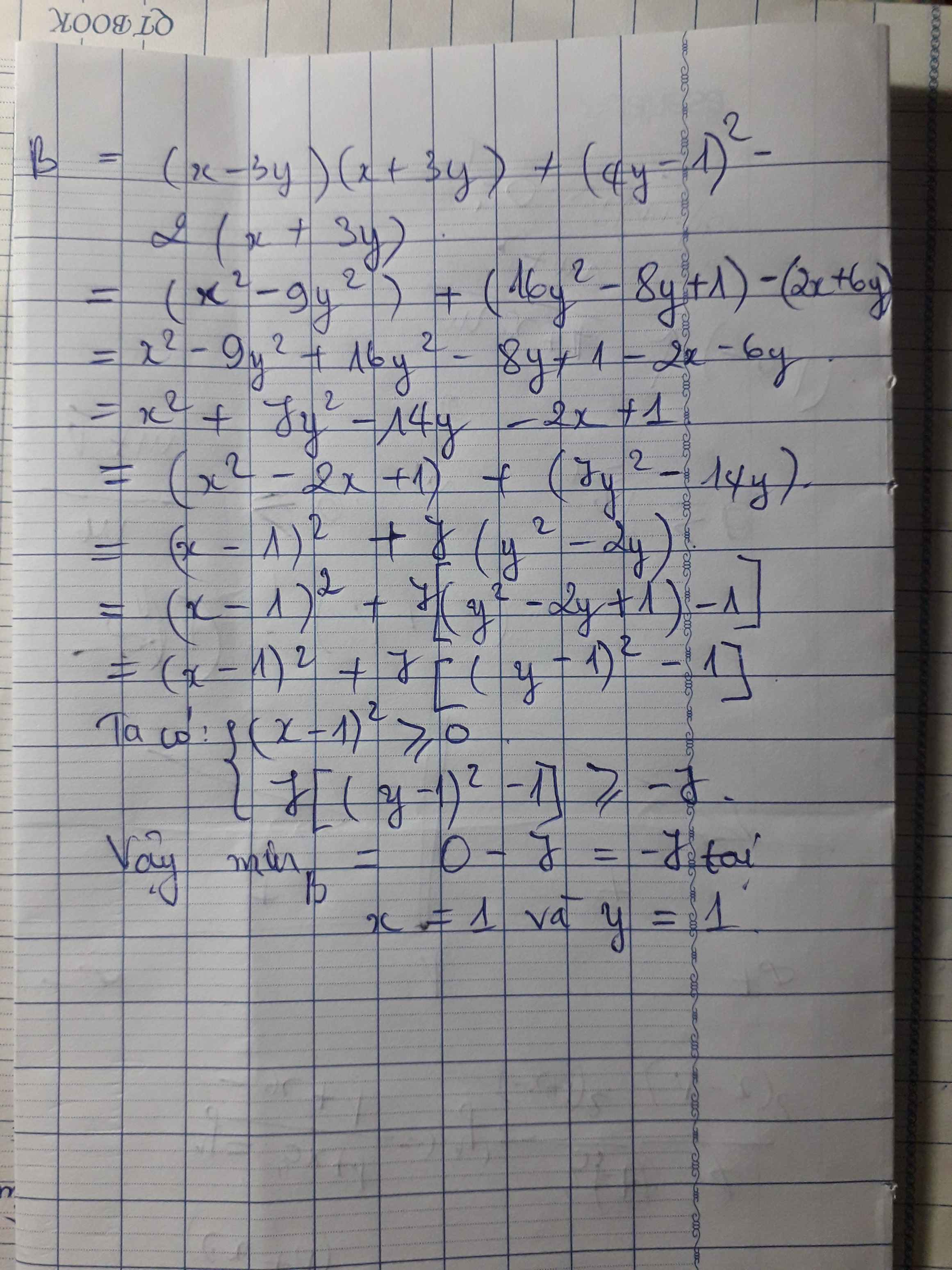Ta có: \(x\ge3y-1\) (gt).

\(\Rightarrow A=x^2+y^2\ge\left(3y-1\right)^2+y^2=9y^2-6y+1+y^2=10y^2-6y+1=10\left(y-\frac{3}{10}\right)^2+\frac{1}{10}\)

\(\Rightarrow A\ge\frac{1}{10}\Rightarrow GTNN\left(A\right)=10\)

Dấu "=" xảy ra khi \(y=\frac{3}{10};x=\frac{1}{10}\).

Sửa giùm mình lại chỗ: \(x\ge1-3y\) nha, mình viết nhầm.

Vs GTNN của A=1/10 không phải là 10

dễ mà

=>x >=1-3y.thay vào bt A= x^2+y^2 >= (1-3y)^2+y^2

đến đây bạn tự giải tiếp nha

x=0;y=1/3

=>A=1/9

\(\left(x+3y\right)^2\ge1\Leftrightarrow\left(1+9\right)\left(x^2+y^2\right)\ge1\Leftrightarrow x^2+y^2\ge\frac{1}{10}\)

theo buniacópky

1=<x+3y=<căn(10*(x^2+y^2))

=>x^2+y^2>=1/10

dùng bunia nha bạn

đáp án là 0.25

biến đổi sẽ được 1-6y+10y^2 

giá trị nhỏ nhất là 0,1 tại x=0,3

dễ mà dốt thé

Tổng của ba đơn thức -4x^{2}y^{2}−4x2y2 ; 2x^{2}y^{2}2x2y2 ; -x^{2}y^{2}−x2y2 là 

giải thích rõ hơn đi bạn

GTNN bằng 5,5 khi y=-3/4

Min =5,5 ..check mk nhá

\(A=x^2+3xy+4y^2\ge4y^2+3y+1\)

\(=\left(4y^2+\frac{2.2y.3}{4}+\frac{9}{16}\right)+\frac{7}{16}\)

\(=\left(2y+\frac{3}{4}\right)^2+\frac{7}{16}\ge\frac{7}{16}\)

\(A=\dfrac{7x^2}{16}+\left(\dfrac{9x^2}{16}+3xy+4y^2\right)\)

\(A=\dfrac{7x^2}{16}+\left(\dfrac{3x}{4}+2y\right)^2\ge\dfrac{7x^2}{16}\ge\dfrac{7.1^2}{16}=\dfrac{7}{16}\)

\(A_{min}=\dfrac{7}{16}\) khi \(\left(x;y\right)=\left(1;-\dfrac{3}{8}\right)\)