Cho (O 9cm) lấy A cách O một khoảng bằng 15cm .Vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm).Độ dài AB là: A. 14cm B 13cm C. 12cm D. 11cm

Những câu hỏi liên quan
Cho hai đường tròn (O;15cm) và (I;13cm) cắt nahu tại A và B.Biết khoảng cách giữa hai tâm là 14cm.Độ dài dây cung AB là
A.12cm B.24cm C.14cm D.28cm
Cho đường tròn (O). Khoảng cách từ O đến dây MN của đường tròn bằng 7cm, ∠ OMN = 45 ° . Trên dây MN lấy một điểm K sao cho MK = 3KN. Độ dài đoạn MK là:
(A)10,5cm
(B) 9cm
(C) 14cm
(D) 12cm
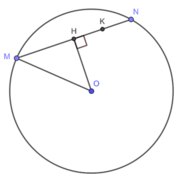
Ta có tam giác MON cân tại O
Mà ∠ OMN = 45 ° suy ra, tam giác OMN vuông cân tại O
OH là đường cao của tam giác MON
Suy ra, OH là đường trung tuyến của tam giác MON
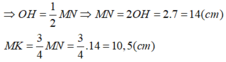
Đáp án: A
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R = 6cm và một điểm A cách O một khoảng 10cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm).
a) Tính độ dài đoạn tiếp tuyến AB.
b) Vẽ cát tuyến ACD, gọi I là trung điểm của đoạn CD. Hỏi khi C chạy trên đường tròn (O) thì I chạy trên đường nào ?
a: Xét ΔOAB vuông tại B có
\(OA^2=OB^2+AB^2\)
hay AB=8(cm)
Đúng 2
Bình luận (0)
Cho đường tròn (O), bán kính R 6 cm và một điểm A cách O một khoảng 10 cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) với đường tròn (O). Lấy điểm C trên đường tròn (O), tia AC cắt đường tròn (O) tại điểm thứ hai là D. Gọi I là trung điểm của CD. a)Tính độ dài đoạn AB.b)Khi C di chuyển trên đường tròn (O) thì I di chuyển trên đường nào?c) Chứng mimh rằng tích AC.AD không đổi khi C thay đổi trên đường tròn (O).
Đọc tiếp
Cho đường tròn (O), bán kính R = 6 cm và một điểm A cách O một khoảng 10 cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) với đường tròn (O). Lấy điểm C trên đường tròn (O), tia AC cắt đường tròn (O) tại điểm thứ hai là D. Gọi I là trung điểm của CD. a)Tính độ dài đoạn AB.
b)Khi C di chuyển trên đường tròn (O) thì I di chuyển trên đường nào?
c) Chứng mimh rằng tích AC.AD không đổi khi C thay đổi trên đường tròn (O).
Mình nói sơ qua nhá:
a) Ta có ΔABO là Δ vuông tại B
Ta tính được AB=8 nhờ vào định lí Py-ta-go
b) Do I là trung điểm của CD nên OI⊥CD, lại suy ra được OI⊥IA
Nên I sẽ chuyển động trên đường tròn đường kính OA (cố định) khi C thay đổi trên đường tròn
c) Chứng minh cho ΔABD∼ΔACB
Suy ra được AC.AD=AB2 không đổi
tk nha bạn
thank you bạn
(^_^)
Đúng 1
Bình luận (1)
cho đường tròn (O) bán kính R8cm và một điểm A cách O một khoảng 10 cm .Từ A vẽ tiếp tuyến AB ( B là tiếp điểm ) với đường tròn (O) .Lấy điểm C trên đường tròn (O) ,Tia AC cắt đường tròn (O) tại D .Gọi I là trung điểm của CD.a Tính độ dài đoạn ABb cm O B A H Cùng thuộc đường trònc Chứng minh rằng tích AC.AD không đổi khi C thay đổi trên đường tròn (O)
Đọc tiếp
cho đường tròn (O) bán kính R=8cm và một điểm A cách O một khoảng 10 cm .Từ A vẽ tiếp tuyến AB ( B là tiếp điểm ) với đường tròn (O) .Lấy điểm C trên đường tròn (O) ,Tia AC cắt đường tròn (O) tại D .Gọi I là trung điểm của CD.
a> Tính độ dài đoạn AB
b> cm O B A H Cùng thuộc đường tròn
c> Chứng minh rằng tích AC.AD không đổi khi C thay đổi trên đường tròn (O)
Cho đường tròn (O), dây AB khác đường kính, lấy I là trung điểm của AB. Đường thẳng OI cắt tiếp tuyến tại A của đường tròn ở điểm C. a) Chứng minh CB là tiếp tuyến của đường tròn. b) Cho bán kính của đường tròn bằng 13cm, AB = 24ccm. Tính độ dài OC.
a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI là đường cao và OI là phân giác của \(\widehat{AOB}\)
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OBC}=\widehat{OAC}=90^0\)
=>CB là tiếp tuyến của (O)
b: I là trung điểm của AB
=>IA=IB=AB/2=12cm
ΔOIA vuông tại I
=>\(OI^2+IA^2=OA^2\)
=>\(OI^2+12^2=13^2\)
=>\(OI^2=169-144=25\)
=>\(OI=\sqrt{25}=5\left(cm\right)\)
Xét ΔOAC vuông tại A có AI là đường cao
nên \(OI\cdot OC=OA^2\)
=>\(OC\cdot5=13^2=169\)
=>OC=33,8(cm)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, bán kính R 6cm và điểm A cách O một khoảng 10cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) và cát tuyến bất kì ACD (C nằm giữa A và D). Gọi I Là trung điểm của CD. a) Tính độ dài AB, số đo góc OAB (làm tròn đến độ). b) Chứng minh bốn điểm A,B,O,I cùng thuộc một đường tròn c) Chứng minh: AC.ADAI^2-IC^2 Từ đó suy ra tích AC.AD không đổi khi C thay đổi trên đường tròn (O).
Đọc tiếp
Cho đường tròn tâm O, bán kính R = 6cm và điểm A cách O một khoảng 10cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) và cát tuyến bất kì ACD (C nằm giữa A và D). Gọi I Là trung điểm của CD.
a) Tính độ dài AB, số đo góc OAB (làm tròn đến độ).
b) Chứng minh bốn điểm A,B,O,I cùng thuộc một đường tròn
c) Chứng minh: \(AC.AD=AI^2-IC^2\)
Từ đó suy ra tích AC.AD không đổi khi C thay đổi trên đường tròn (O).
Cho đường tròn (O; 5cm) và điểm A nằm ngoài đường tròn cách O một khoảng 7cm. Vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Khi đó AB bằng
\(AB=2\sqrt{6}\left(cm\right)\)
Đúng 0
Bình luận (0)
cho đường tròn(o) bán kính R6cm và một điểm A cách O khoảng 10cm. Từ A vẽ tiếp tuyến AB(B là tiếp điểm) với đường tròn tâm O. lấy điểm C trên đường tròn tâm O, tia AC cắt đường tròn tâm O tại điểm thứ hai là D. gọi I là trung điểm của CDa/ tính độ dài đoạn thẳng ABb/ khi C di chuyển trên đường tròn(o) thì I di chuyển trên đường nào?c/ cm rằng tích AC.AD khồng đổi khi c thay đổi trên (o)
Đọc tiếp
cho đường tròn(o) bán kính R=6cm và một điểm A cách O khoảng 10cm. Từ A vẽ tiếp tuyến AB(B là tiếp điểm) với đường tròn tâm O. lấy điểm C trên đường tròn tâm O, tia AC cắt đường tròn tâm O tại điểm thứ hai là D. gọi I là trung điểm của CD
a/ tính độ dài đoạn thẳng AB
b/ khi C di chuyển trên đường tròn(o) thì I di chuyển trên đường nào?
c/ cm rằng tích AC.AD khồng đổi khi c thay đổi trên (o)














