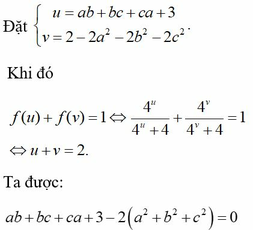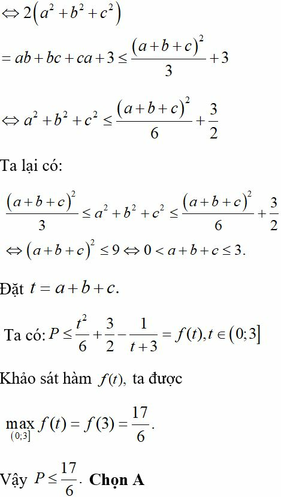Chob>a>0 thỏa mãn:2a2+2b2=5ab Khi đó giá trị của biểu thức:2b/a-b +1 là

Những câu hỏi liên quan
Chob>a>0 thỏa mãn:2a2+2b2=5ab Khi đó giá trị của biểu thức:2b/a-b +1 là
cho b>a>0 thỏa mãn : 2a2+2b2=5ab. khi đó giá trị của biểu thức A = \(A=\frac{2b}{a-b}+1\)là
Có: 2a2 + 2b2 = 5ab => 2(a2 + b2) = 5ab => a2 + b2 = \(\frac{5}{2}\)ab
\(A=\frac{2b}{a-b}+1=\frac{2b+a-b}{a-b}=\frac{a+b}{a-b}=\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\frac{a^2+b^2+2ab}{a^2+b^2-2ab}=\frac{\frac{5}{2}ab+2ab}{\frac{5}{2}ab-2ab}=\frac{\frac{9}{2}ab}{\frac{1}{2}ab}=9\)
Vậy A = 9
Đúng 0
Bình luận (0)
Nhận xét: vì b>a>0 nên a-b < 0 và 2b>a-b nên A<0.
Bình phương hai vế:
A2 = 9. nên A = 3; A = -3. Đáp số: A = -3
Đúng 0
Bình luận (0)
Cho các số thực a, b, x 0 và b, x ≠ 1 thỏa mãn
log
x
a
+
2
b
3
log
x
a
+
log
x
b
. Tính giá trị của biểu thức
P
2
a
2
+
3
a
b
+...
Đọc tiếp
Cho các số thực a, b, x > 0 và b, x ≠ 1 thỏa mãn log x a + 2 b 3 = log x a + log x b . Tính giá trị của biểu thức P = 2 a 2 + 3 a b + b 2 a + 2 b - 2 khi a > b
A. 2
B. 2 3
C. 10 27
D. 5 4
Cho các số thực dương a,b,c thỏa mãn
f
a
b
+
b
c
+
c
a
+
3
+
f
2
-
2
a
2
-
2
b
2...
Đọc tiếp
Cho các số thực dương a,b,c thỏa mãn f a b + b c + c a + 3 + f 2 - 2 a 2 - 2 b 2 - 2 c 2 = 1 với hàm số f x = 4 x 4 x + 4 Giá trị lớn nhất của biểu thức P = a 2 + b 2 + c 2 - 1 a + b + c + 3 bằng
A. 17 6
B. 3
C. 13 6
D. 13 4
1 Cho x,y là các số thỏa mãn I x-3 I + (y+4)^2 = 0
2 Số các giá trị nguyên của x thỏa mãn
2(IxI- 5) ( x^2 -9) =0
3 Nếu 1/2 của a bằng 2b thì 9/8a = kb . Vậy kb =
4 Số giá trị của x thỏa mãn
x^2 +7x +12 = 0
5 Biết (a+1) (b+1) = 551 khi đó giá trị của biểu thức ab+a+b = ?
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
Đọc tiếp
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
Cho \(a>0\) , \(b>0\) thỏa mãn: \(\log_{3a+2b+1}\left(9a^2+b^2+1\right)+\log_{6ab+1}\left(3a+2b+1\right)=2\) .
Tính giá trị của biểu thức: \(P=a+2b\)
\(a;b>0\Rightarrow3a+2b+1>1\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\) đồng biến
Mà \(9a^2+b^2\ge2\sqrt{9a^2b^2}=6ab\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)\)
\(\Rightarrow log_{3a+2b+1}\left(9a^2+b^2+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge log_{3a+2b+1}\left(6ab+1\right)+log_{6ab+1}\left(3a+2b+1\right)\ge2\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}log_{6ab+1}\left(3a+2b+1\right)=1\\3a=b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6ab+1=3a+2b+1\\b=3a\end{matrix}\right.\)
\(\Rightarrow18a^2+1=3a+6a+1\)
\(\Leftrightarrow18a^2-9a=0\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{3}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Bài 6:Cho các số a,b,c khác 0 thỏa mãn
2a-2b+9c=9 Tính giá trị của M=a+3c/a+4b-3c
a-2b+6c=5
Bài 7 Cho a,b>0 thỏa mãn a+b=3.Tìm giá trị nhỏ nhất của biểu thức T=a^2+4/a+b^2/b+3
Bài 6:Cho các số a,b,c khác 0 thỏa mãn
2a-2b+9c=9 Tính giá trị của M=a+3c/a+4b-3c
a-2b+6c=5
Bài 7 Cho a,b>0 thỏa mãn a+b=3.Tìm giá trị nhỏ nhất của biểu thức T=a^2+4/a+b^2/b+3