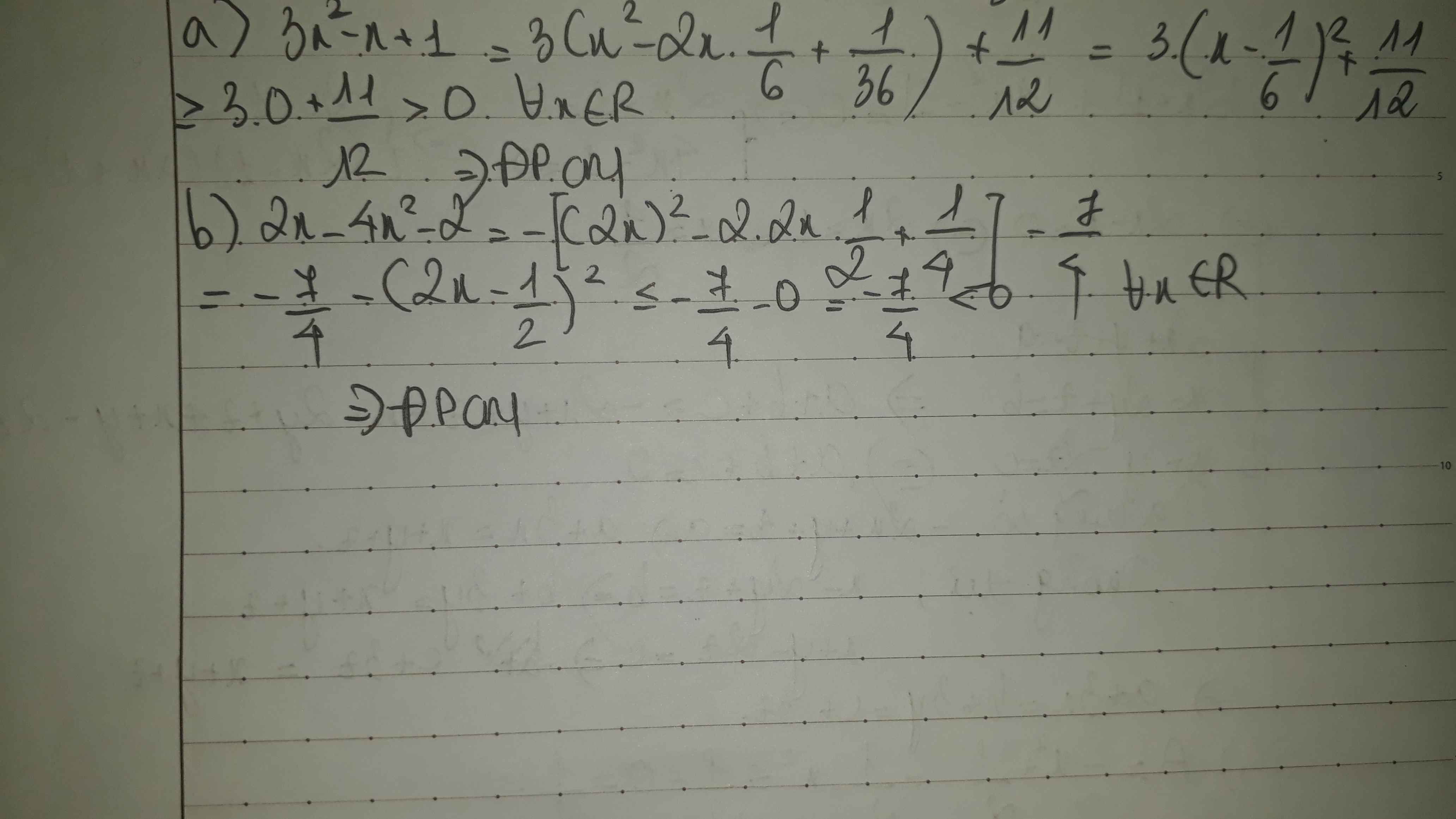Lời giải:

a.

\(3x^2+2y\vdots 11\Leftrightarrow 5(3x^2+2y)\vdots 11\)

$\Leftrightarrow 15x^2+10y\vdots 11$

$\Leftrightarrow 15x^2+10y-22y\vdots 11$

$\Leftrightarrow 15x^2-12y\vdots 11$ (đpcm)

b.

$2x+3y^2\vdots 7$

$\Leftrightarrow 3(2x+3y^2)\vdots 7$

$\Leftrightarrow 6x+9y^2\vdots 7$

$\Leftrightarrow 6x+9y^2+7y^2\vdots 7$

$\Leftrightarrow 6x+16y^2\vdots 7$ (đpcm)

\(=3^{x+1}\left(1+3+3^2\right)+...+3^{x+10}\left(1+3+3^2\right)=\)

\(=3^x.3.13+...+3^{x+9}.3.13=\)

\(39\left(3^x+...+3^{x+9}\right)⋮39\)

Bài 1: 

a) Ta có: \(\left(2x-1\right)^{20}=\left(2x-1\right)^{18}\)

\(\Leftrightarrow\left(2x-1\right)^{20}-\left(2x-1\right)^{18}=0\)

\(\Leftrightarrow\left(2x-1\right)^{18}\left[\left(2x-1\right)^2-1\right]=0\)

\(\Leftrightarrow\left(2x-1\right)^{18}\cdot\left(2x-2\right)\cdot2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=1\end{matrix}\right.\)

b) Ta có: \(\left(2x-3\right)^2=9\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)

c) Ta có: \(\left(x-5\right)^2=\left(1-3x\right)^2\)

\(\Leftrightarrow\left(x-5\right)^2-\left(3x-1\right)^2=0\)

\(\Leftrightarrow\left(x-5-3x+1\right)\left(x-5+3x-1\right)=0\)

\(\Leftrightarrow\left(-2x-4\right)\left(4x-6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{3}{2}\end{matrix}\right.\)

Bài 2: 

a) \(15^{20}-15^{19}=15^{19}\left(15-1\right)=15^{19}\cdot14⋮14\)

b) \(3^{20}+3^{21}+3^{22}=3^{20}\left(1+3+3^2\right)=3^{20}\cdot13⋮13\)

c) \(3+3^2+3^3+...+3^{2007}\)

\(=3\left(1+3+3^2\right)+...+3^{2005}\left(1+3+3^2\right)\)

\(=13\left(3+...+3^{2005}\right)⋮13\)

\(3^{x-1}.7+3^{x-1}.2=9\\ 3^{x-1}.\left(7+2\right)=9\\ 3^{x-1}.9=9\\ 3^{x-1}=\dfrac{9}{9}=1\\ Mà:3^0=1\\ Nên:x-1=0\\ Vậy:x=0+1=1\\ ---\\ P=2+2^2+2^3+...+2^{65}+2^{66}=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{64}+2^{65}+2^{66}\right)\\ =2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{64}\left(1+2+2^2\right)\\ =2.7+2^4.7+...+2^{64}.7\\ =\left(2+2^4+....+2^{64}\right).7⋮7\left(đpcm\right)\)

+)
\(3^{x-1}.7+3^{x-1}.2=9\)
\(3^{x-1}.\left(7+2\right)=9\)
\(3^{x-1}.9=9\)
\(3^{x-1}=9:9\)
\(3^{x-1}=1\)
⇔\(3^{x-1}=3^0\)
⇒\(x-1=0\)
\(x=0+1\)
\(x=1\)
Vậy \(x=1\)

+)
\(2+2^2+2^3+...+2^{65}+2^{66}\)
Vì \(2+2^2+2^3=14\) mà \(14\)⋮\(7\)
⇒Ta nhóm 3 số với nhau
Ta có:
\(\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{64}+2^{65}+2^{66}\right)\)
\(\left(2+2^2+2^3\right)+2^3.\left(2+2^2+2^3\right)+...+2^{63}.\left(2+2^2+2^3\right)\)
\(14.1+14.2^3+...+14.2^{63}\)
\(14.\left(1+2^3+...+2^{63}\right)\)
Do \(14\)⋮\(7\) nên \(P=14.\left(2+2^3+...+2^{63}\right)\)⋮\(7\)

Xin tick

bài 1: = 100-( 120 - 6.4)

         = 100 - (120-24)

         = 100 -  96

        =   4

bài 2: 3x+13=-2

          3x= (-2)-13

          3x=  -15

           x=  -15 : 3

          x=    -5

   bài 3: ko bt :)))

đúng :))

oke thanks bro:>

mà có đúng khơm zị.-.

1. \(S=\left(1-\frac{1}{2^2}\right).\left(1-\frac{1}{3^2}\right)...\left(1-\frac{1}{100^2}\right)\)

\(S=\left(1-\frac{1}{4}\right).\left(1-\frac{1}{9}\right)...\left(1-\frac{1}{10000}\right)\)

\(S=\frac{3}{4}.\frac{8}{9}...\frac{9999}{10000}\)

\(S=\frac{1.3}{2.2}.\frac{2.4}{3.3}...\frac{99.101}{100.100}\)

\(S=\frac{1.2...99}{2.3...100}.\frac{3.4...101}{2.3...100}\)

\(S=\frac{1}{100}.\frac{101}{2}\)

\(S=\frac{101}{200}\)

2. 

Vì 3x - 5y \(⋮\)23

\(\Rightarrow\)6 . ( 3x - 5y ) \(⋮\)23

Ta có : 6 . ( 3x - 5y ) + ( 5x - 16y )

\(\Leftrightarrow\)( 18x - 30y ) + ( 5x - 16y )

\(\Leftrightarrow\)23x - 46y

\(\Leftrightarrow\)23 . ( x - 2y ) \(⋮\)23

Vì 18x - 30y \(⋮\)23 mà ( 5 ; 23 ) = 1

\(\Rightarrow\)5x - 16y \(⋮\)23

SKT_NTT sai câu 1 rồi từ đoạn thứ 2

bn ơi đây là toán lớp mấy vậy????

toán này chắc toán lớp 4 hoặc lớp 5 rồi

bạn hk lớp mấy 

Giống toán lớp 7 vcl