Giải giúp mình câu 39- 40 với mn. Mình cảm ơn nhìu


Những câu hỏi liên quan
mn chỉ mình với câu tính diện tích hình vuông có chu vi là 280 ? mn giải giúp mình ạ cảm ơn mn nhìu
TL:
Tìm 1 cạnh của hình vuông: 280 : 4 = 70 ( ................ mik ko biết đơn vị là gì hết bạn ơi ! )
Diện tích hình vuông đó là: 70 x 70 = 4900 ( ..........2 )
Đáp số: 4900 .....2
Chúc bạn học tốt!
k mik nha!
Cho ΔABO cân tại A, kẻ AH vuông góc với BO tại H. Chứng minh ΔAHB = ΔAHO
Mọi người giúp mình giải câu này nha ^^ Cảm ơn mn nhìu ^^
có: tam giác ABO cân tại A (gt)
=> AB=AO (tính chất tam giác cân)
Có: AH vuông góc BO (gt)
=> góc AHB = góc AHO (tính chất đường vuông góc)
Xét tam giác AHB và tam giác AHO có
goc AHB = góc AHO (cmt)
AB = AO (cmt)
AH chung
=> tam giác AHB = tam giác AHO (cạnh huyền - cạnh góc vuông)
Đúng 1
Bình luận (0)

mn giải giúp mình vs
mình cảm ơn rất nhìu
Bạn tự vẽ hình nha
Nối BN
+ Diện tích tam giác AMN = diện tích tam giác BMN ( vì đáy AM = BM và có chung đường cao hạ từ N xuống )
⇒ Diện tích tam giác BMN = 4cm2
⇒ Diện tích tam giác ANB = 8cm2
Diện tích tam giác ABN = diện tích tam giác BCN ( vì đáy AN = CN và có chung đường cao hạ từ B xuống )
⇒ Diện tích tam giác BNC = 8cm2
⇒ Diện tích tam giác ABC = 8 + 8 = 16 ( cm2 )
Vậy diện tích tam giác ABC = 16 cm2
Đúng 3
Bình luận (1)
Mình cảm ơn các bạn nhìu lắm vì giúp mình trả lời một số câu hỏi ôn thi!!!!!! Mình cảm ơn các bạn nhìu nhìu lắm lắm nha!!!!!!!!!!!!!![]()
Ko! Còn mấy câu khác nữa!!!!! Nhưng mấy câu ấy cô trả lời hết rùi!!!!! Còn mấy câu mà mình hỏi mấy bạn là những câu hỏi tư duy, học sinh phải tự làm!!!!!!!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
các bạn giúp mình câu này nhé đc hông?
(32+128)=32:4=8+32=40
đúng hay sai ạ? cảm ơn mn nhìu :3
thế tóm lại là đúng hay sai :v
Mn ơi giúp mik với, please please lm ơn giúp mik nka, huhu giúp mik đuy, mik cảm ơn mn rất rất nhìu nhìu lunnnnnnn. Giúp mình nha! Thank kiuuu mn

Giúp mình với ạ cảm ơn mn nhìu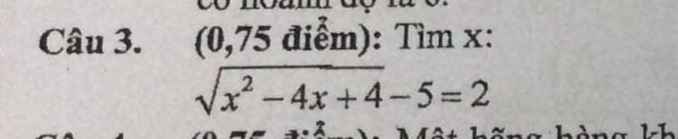
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=7\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Ta có: \(\sqrt{x^2-4x+4}-5=2\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cứu mình với mình ko biết làm bài này với lại mình đang cần gấp giúp mình giải chi tiết nhé mình cảm ơn nhìu lắm lun ế .Cho tam giác ABC, trên BC lấy điểm chính giữa M .Nối A với M.Trên am lấy điểm N sao cho MN 1/3 x AM.Nối B với N cắt AC tại D.a.Kể tên các hình tam giác có trong hình vẽ .b.Diện tích hình tam giác MBN bằng 5 cm2.Tính diện tích hình tam giác ABM và diện tích hình tam giác ABC( Các bạn ơi có vẽ hình nhưng mình ko biết vẽ nhớ vẽ giúp mình nhớ mình đội ơn nhìu ) mình cảm ơn cảm ơn n...
Đọc tiếp
cứu mình với mình ko biết làm bài này với lại mình đang cần gấp giúp mình giải chi tiết nhé mình cảm ơn nhìu lắm lun ế .
Cho tam giác ABC, trên BC lấy điểm chính giữa M .Nối A với M.Trên am lấy điểm N sao cho MN =1/3 x AM.Nối B với N cắt AC tại D.
a.Kể tên các hình tam giác có trong hình vẽ .
b.Diện tích hình tam giác MBN bằng 5 cm2.Tính diện tích hình tam giác ABM và diện tích hình tam giác ABC
( Các bạn ơi có vẽ hình nhưng mình ko biết vẽ nhớ vẽ giúp mình nhớ mình đội ơn nhìu ) mình cảm ơn cảm ơn nhìu! giúp mình giải nhanh nhé !
mn giải giúp mik vs ạ, giải chi tiết ra luôn, mình phải nộp trong hôm nay rùi ạ, cảm ơn mn nhìu


Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)
Đúng 1
Bình luận (0)






















