Tìm các số nguyên x thỏa mãn I-12.x+7I=40
Số các số nguyên x thỏa mãn: (IxI - 5)(x3 - 8).Ix - 7I = 0 là: ............
\(\Rightarrow\left(\left|x\right|-5\right)=0;\left(x3-8\right)=0;\left|x-7\right|=0\)
\(\left|x\right|-5=0\)
\(\left|x\right|=5\Rightarrow x=5và-5\)
\(x3-8=0\)
\(3x=8\)
\(x=\frac{8}{3}\)
\(\left|x-7\right|=0\)
\(x-7=0\)
\(x=7\)
(IxI - 5)(x3 - 8).Ix - 7I = 0 =>(IxI - 5)=0 hc (x3 - 8)=0 hc Ix - 7I = 0
=> IxI= 5 ; x3 =8 ; x - 7 = 0 hc 7-X=0
=>x=5 hc x=-5 ; x=8/3 ; x=7
Tìm các số nguyên x thỏa mãn:
18 ⁝ x; 12 ⁝ x , x lớn nhất
120 : ( 2x - 6) = 12
Tìm các số nguyên x thỏa mãn:
18 ⁝ x; 12 ⁝ x , x lớn nhất
120 : ( 2x - 6) = 12
Tìm các số nguyên x,y thỏa mãn : xy +12=x+y
Lời giải:
$xy+12=x+y$
$\Rightarrow xy-x-y=-12$
$\Rightarrow x(y-1)-y=-12$
$\Rightarrow x(y-1)-(y-1)=-11$
$\Rightarrow (y-1)(x-1)=-11$
Do $x,y$ nguyên nên $x-1,y-1$ cũng nguyên. Ta có bảng: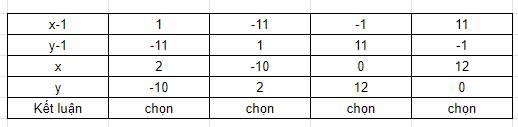
a, Tìm tất cả các số nguyên x thỏa mãn -11<x<9. Tính tổng tất cả các số nguyên vừa tìm đc
b,Tìm tất cả các số nguyên x thỏa mãn -9<x<10.Tính tổng các số nguyên vừa tìm đc
c,Tìm tất cả các số nguyên x thỏa mãn -15<x<16.Tính tổng tất cả các số nguyên vừa tìm đc
Phần b và c là dấu lớn hơn hoặc bằng nhé !!
MN GIÚP MÌNH VỚI Ạ !!!!
a)
Các số nguyên x thỏa mãn là:
\(x\in\left\{-10;-9;-8;-7;-6;-5;-4;-3;-2;-1;0;1;2;3;4;5;6;7;8\right\}\)
Tổng các số nguyên trên là:
\((8-10).19:2=-19\)
b)
Các số nguyên x thỏa mãn là:
\(x\in\left\{-9;-8;-7;-6;-5;-4;-3;-2;-1;...;6;7;8;9;10\right\}\)
Tổng các số trên là:
\((10-9).20:2=10\)
c) Các số nguyên x thỏa mãn là:
\(x\in\left\{-15;-14;-13;-12;-11;-10;-9;-8;-7;-6;-5;...;12;13;14;15;16\right\}\)
Tổng các số nguyên đó là:
\((16-15).32:2=16\)
Tìm tất cả các cặp số nguyên(x,y)thỏa mãn:2^x+1.3^y=12^x
Ta có : \(2^{x+1}.3^y=12^x\)
\(\Leftrightarrow3^y=\dfrac{12^x}{2^{x+1}}=\dfrac{3^x.4^x}{2^{x+1}}=\dfrac{3^x.2^{2x}}{2^{x+1}}=3^x.2^{2x}:2^{x+1}=3^x.2^{x-1}\)
\(\Leftrightarrow\dfrac{3^y}{3^x}=2^{x-1}\)
\(\Leftrightarrow3^{y-x}=2^{x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}y-x=0\\x-1=0\end{matrix}\right.\Leftrightarrow x=y=1\)(tm)
Vậy (x;y) = (1;1) nghiệm của phương trình trên
tìm các số nguyên x,y thỏa mãn:6xy-10x+3y=12
2) Tìm các số nguyên thỏa mãn: x. (y + 1) + y = 12
=>xy+x+y=12
=>y(x+1)+x+1=13
=>(x+1)(y+1)=13
=>\(\left(x+1;y+1\right)\in\left\{\left(1;13\right);\left(13;1\right);\left(-1;-13\right);\left(-13;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;12\right);\left(12;0\right);\left(-2;-14\right);\left(-14;-2\right)\right\}\)
Tập hợp các số nguyên x thỏa mãn |( x - 23)( x + 12)| = 0 là {}
Số nguyên x thỏa mãn x - ( -25 - 17 - x ) = 6 + x là
Tập hợp các số nguyên x thỏa mãn | -17 - x | = 2 là {}
|(x - 23)(x + 12)| = 0
Th1: x - 23 = 0 => x = 23
Th2: x + 12= 0 => x= -12
|( x - 23)( x + 12)| =0
=> x-23=x+12 hoặc x-23=-x+12
sau đó gom x lại áp dugnj quy tắc chuyển vế là ra