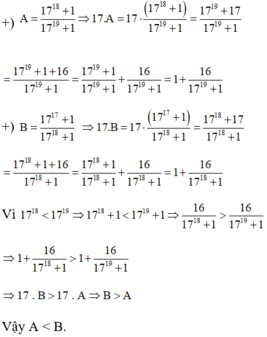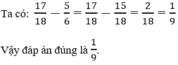a) A < B              

b) C > D

a) Ta có :

\(\frac{1717\div101}{1919\div101}=\frac{17}{19}\)

Vậy : \(\frac{17}{19}=\frac{1717}{1919}\)

b) Ta có :

4²²² = ( 2²)²²² = 2⁴⁴⁴

Do 2⁴⁴⁴ = 2⁴⁴⁴

Suy ra 2⁴⁴⁴ = 4²²²

Vậy : 2⁴⁴⁴ = 4²²²

Thanks nha

Ta có \(\frac{-17}{-19}=\frac{\left(-17\right).\left(-101\right)}{\left(-19\right).\left(-101\right)}=\frac{1717}{1919}\)

mà \(\frac{1717}{1919}

2,\(\frac{189}{1297}\) và \(\frac{317}{1146}\)

Xét phân số trung gian là \(\frac{189}{1146}\) . Ta có:

\(\frac{189}{1297}\)< \(\frac{189}{1146}\)

\(\frac{189}{1146}\)< \(\frac{317}{1146}\)

\(\Rightarrow\)\(\frac{189}{1297}\) < \(\frac{317}{1146}\)(tính chất bắc cầu)

Lời giải:

\(\frac{1719}{3976}=\frac{1}{2+\frac{538}{1719}}=\frac{1}{2+\frac{1}{3+\frac{105}{538}}}=\frac{1}{2+\frac{1}{3+\frac{1}{5+\frac{13}{105}}}}=\frac{1}{2+\frac{1}{3+\frac{1}{5+\frac{1}{8+\frac{1}{13}}}}}\)

$\Rightarrow a=8; b=13$

\(\dfrac{1719}{3976}=\dfrac{1}{\dfrac{3976}{1719}}=\dfrac{1}{2+\dfrac{538}{1719}}=\dfrac{1}{2+\dfrac{1}{\dfrac{1719}{538}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{105}{538}}}\)

\(=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{\dfrac{538}{105}}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{13}{105}}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{1}{\dfrac{105}{13}}}}}\)

\(=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{1}{8+\dfrac{1}{13}}}}}\)

1719​=17193976​1​=2+1719538​1​=2+5381719​1​1​=2+3+538105​1​1​

=12+13+1538105=12+13+15+13105=12+13+15+110513=2+3+105538​1​1​1​=2+3+5+10513​1​1​1​=2+3+5+13105​1​1​1​1​

=12+13+15+18+113=2+3+5+8+131​1​1​1​1​
 

A=17/18+1718/1718+171717/181818

\(A=\frac{17}{18}+\frac{1717}{1818}+\frac{171717}{181818}+...+\frac{1717..17}{1818...18}\)(2018 số 17 và 18) 

\(=\frac{17}{18}+\frac{17.101}{18.101}+\frac{17.10101}{18.10101}+...+\frac{17.1010...01}{18.1010...01}\)(2017 cặp số 10 liên tiếp và dư 1 số 1)

\(=\frac{17}{18}+\frac{17}{18}+\frac{17}{18}+...+\frac{17}{18}\left(2018\text{ số hạng}\right)\)

\(=\frac{17}{18}.2018=\frac{17153}{9}\)

                                                  Bài giải

\(A=\frac{17}{18}+\frac{1717}{1818}+\frac{171717}{181818}+\frac{17...17}{18...18}\text{ ( 2018 chữ số17 và 18 ) }\)

\(A=\frac{17}{18}+\frac{17\cdot101}{18\cdot101}+...+\frac{17\cdot1010...1}{18\cdot1010...1}\) ( Có 2017 cặp số 10 và 1 số 1 )

\(A=\frac{17}{18}+\frac{17}{18}+...+\frac{17}{18}\)( Có 1009 số hạng )

\(A=\frac{17}{18}\cdot1009\)

\(A=\frac{17153}{18}\)

Hướng dẫn giải:

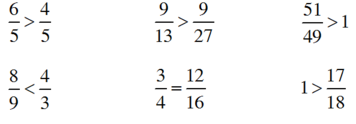
Giải thích:

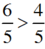+  vì cùng có mẫu bằng 5, tử số 6 > 4.

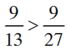+  vì có cùng tử số, mẫu số 13 < 27.

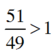+  vì tử số 51 > mẫu số = 49.

+ 

+ 

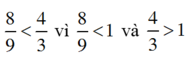
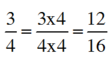
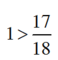+  vì tử số bằng 17 < mẫu số bằng 18.

Đáp án A

\(A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}\)

\(\dfrac{1}{2.2}< \dfrac{1}{1.2}=1-\dfrac{1}{2}\)

\(\dfrac{1}{3.3}< \dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)

\(\dfrac{1}{4.4}< \dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4}\)

...

\(\dfrac{1}{2009.2009}< \dfrac{1}{2008.2009}=\dfrac{1}{2008}-\dfrac{1}{2009}\)

\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...\dfrac{1}{2008}-\dfrac{1}{2009}=1-\dfrac{1}{2009}< 1\)

\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}< 1\)

Ta có:

\(\dfrac{1}{2\times2}+\dfrac{1}{3\times3}+\dfrac{1}{4\times4}+...+\dfrac{1}{2009\times2009}< \dfrac{1}{1\times2}+\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+...+\dfrac{1}{2008\times2009}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2008}-\dfrac{1}{2009}=1-\dfrac{1}{2009}< 1\)