Cho tam giác ABC biết rằng số đo các góc A ^ ; B ^ ; C ^ tỉ lệ với 2; 3; 4. Tính C ^
A. 60 °
B. 90 °
C. 40 °
D. 80 °
tam giác ABC có số đo các góc A,B,C tỉ lệ với 3,5,7 .Tính số đo các góc của tam giác ABC.(Biết rằng tổng số đo góc tong 1 tam giác bằng 1 tam giác
Tổng số đo các góc của hình tam giác luôn bằng 360 độ
Số đo của góc A là:360:(3+5+7)x3=72 độ
Số đo của góc B là:72:3x5=120 độ
Số đo của góc C là:360-120-72=168 độ
Góc A = 72o
Góc B = 120o
Góc C = 168o
tam giác ABC có số đo các góc A,B,C tỉ lệ với 3,5,7 .Tính số đo các góc của tam giác ABC biết rằng tổng số đo ba trong 1 tam giác = 180o
Cho tam giác ABCvà đường cao AH, H thuộc BC . Biết rằng góc BAH=góc BCA.
a) Chứng minh rằng tam giác ABC là tam giác vuông.
b) Biết rằng số đo góĉ ABC bằng trung bình cộng của hai góc ̂BACvà góc ACB. Tính số đo các góc của tam giácABC.
Tam giác ABC có số đo các góc A, B, C tỉ lệ với 3; 5; 7. Tính số đo các góc của tam giác ABC, biết rằng tổng số đo ba góc trong một tam giác bằng 1800 .
Giúp mình với
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)
Tam giác ABC có số đo góc A,B,C tỉ lệ với 3;5;7.Tính số đo các góc của tam giác ABC (biết rằng tổng số đo 3 góc trong 1 tam giác =180 độ)
Tam giác ABC có số đo 3 góc A, B , C tỉ lệ với 3; 5 ;7. Tính số đo các góc của tam giác ABC (biết rằng tổng số đo 3 góc trong một tam giác bằng 180o)
Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
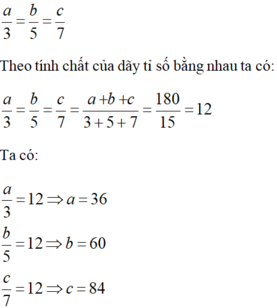
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o
Tam giác ABC có số đo các góc A,B,C biết rằng các cạnh tỷ lệ với 3:4:5.Tính số đo các góc của tam giác ABC
đề sai bạn ơi, các góc tỉ lệ chứ cạnh cđg
theo đề bài ta có :
A/3 = B/4 = C/5
=> A+B+C/3+4+5 = A/3=B/4=C/5
A+B+C = 180
=> 180/12 = A/3 = B/4 = C/5
=> 15 = A/3 = B/4 = C/5
=> A = 45 ; B = 60; C = 75
Gọi 3k, 4k, 5k lần lượt là các cạnh của tam giác ABC \(\left(k>0;k\inℝ\right)\)
Áp dụng định lí pythagore đảo vào tam giác ABC:
Vì \(\left(5k\right)^2=25k^2=9k^2+16k^2=\left(3k\right)^2+\left(4k\right)^2\)
Suy ra: tam giác ABC là tam giác vuông có độ dài cạnh huyền là 5k, độ dài 2 cạnh góc vuông là 3k, 4k
Với tam giác ABC vuông tại A, thì: \(\widehat{A}=90^0\)
Giả sử: AB = 3k ; AC = 4k
\(\sin B=\frac{AC}{BC}=\frac{4k}{5k}=\frac{4}{5}\Rightarrow\widehat{B}\approx53^0\)
Vì tổng các góc \(\widehat{A}=90^0\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^0\)
\(\Rightarrow\widehat{C}=90^0-\widehat{B}=90^0-53^0=37^0\)
Vậy 3 góc trong tam giác có số đo là: \(90^0;37^0;53^0\)
HỌC TỐT!
Gọi 3 góc của tam giác tại A ; B ; C lần lượt là a ; b và c
\(\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)
\(\Rightarrow\hept{\begin{cases}a=45^o\\b=60^o\\c=75^o\end{cases}}\)
Nguồn: Silver bullet
Cho tam giác ABC bằng tam giác DEF.Tính số đo các góc của tam giác ABC ,biết rằng:
Góc A=1/2 góc F,1/2 góc B=1/3 góc F
Cho tam giác ABC, biết rằng số đo các góc A ^ , B ^ , C ^ tỉ lệ với 2, 3, 4. Số đo của góc A là:
A. 20 °
B. 40 °
C. 60 °
D. 80 °

Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
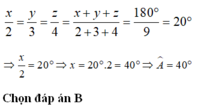
Tam giác ABC có số đo các góc A, B, C tỉ lệ 3 : 5 : 7. Tính số đo các góc của tam giác ABC (Biết rằng tổng số đo ba góc trong một tam giác bằng \(180^0\))
Theo đề bài ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^o}{15}=12^o\)
\(\Rightarrow\widehat{A}=12^o.3=36^o\)
\(\widehat{B}=12^o.5=60^o\)
\(\widehat{C}=12^o.7=84^o\)
nếu số đo (độ) các góc của tam giác ABC là A , B , C (độ) thì theo điều kiện bài ra và tính chất của dãy tỉ số bằng nhau , ta có \(\dfrac{A}{3}=\dfrac{B}{5}=\dfrac{C}{7}=\dfrac{A+B+C}{3+5+7}=\dfrac{180}{15}=12\)
vậy : A = 3 . 12 = 36
B = 5 . 12 = 60
C = 7 . 12 = 84
=> A = 36 (độ) ; B = 60 (độ) ; C = 84 (độ)
Gọi số đo của các góc A,B,C trong tam giác ABC lần lượt là là a,b,c
Ta có: \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\) và tổng ba góc là 180o
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{180^o}{15}=12^o\)
+) Nếu \(\dfrac{a}{3}=12\)⇒ a= 36o
+)Nếu \(\dfrac{b}{5}\)=12⇒b=60o
+)Nếu \(\dfrac{c}{7}\)=12⇒c=84o
Vậy góc A bằng 36o, góc B bằng 60o, góc C bằng 84o