tìm x
[(x-3)^2+8].2=18.giá trị của x là
A x =4
B x=3
C x=8
D x=4 và x=8
A=\(\left(\dfrac{x}{x+2}+\dfrac{x^3-8}{x^3+8}.\dfrac{x^2-2x+4}{4-x^2}\right):\dfrac{4}{x+2}\)
a) tìm đkxđ và rút gọn biểu thức A
b) tìm x để A=3
c) tìm x để a<1
d) tính giá trị của A khi |x| =\(\dfrac{1}{2}\)
Với x∈Z và x + 5 = 3, giá trị của x là:
A. (- 8)
B. 2
C. 8
D. (- 2)
Với x∈Z và x + 5 = 3, giá trị của x là:
A. (- 8)
B. 2
C. 8
D. (- 2)
Câu 1. Giá trị của x thỏa mãn \(\sqrt{2x}=6\) là
A. x=3 B. x=18 C. x=6 D. x =1
Câu 2. Giá trị của tham số m để hai đường thẳng \(y=\left(m-1\right)x+2\) (m ≠ 1) và y = 3x -1 cắt nhau là
A. m = -4 B. m ≠ -4 C. m = 4 D. m ≠ 4
Câu 3. Cho hai đường thẳng \(y=12x+5-m\) và \(y=3x+3+m\). Để hai đường thẳng này cắt nhau tại một điểm trên trục tung thì giá trị của m là
A. m = -1 B. m = -3 C. m = 1 D. m = 5
cho biểu thức P=x2-x-18/x2-9+2/x-3-4/x+3
a rút gọn biểu thứcp
b,tìmcác giá trị của x để p=2/3
c,tìm các giá trị nguyên của x để Pnhận giá trị nguyên
a: \(P=\dfrac{x^2-x-18+2x+6-4x+12}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2-3x}{\left(x-3\right)\left(x+3\right)}=\dfrac{x}{x+3}\)
b: P=2/3
=>x/(x+3)=2/3
=>3x=2x+6
=>x=6(nhận)
c: P nguyên
=>x chia hết cho x+3
=>x+3-3 chia hết cho x+3
=>x+3 thuộc {1;-1;2;-2}
=>x thuộc {-2;-4;-1;-5}
Cho biểu thức A=(\(\dfrac{x^2}{x^3-4x}+\dfrac{6}{6-3x}+\dfrac{1}{x+2}\)):(x-2 + \(\dfrac{10-x^2}{x+2}\))
a)Rút gọn A
b)Tính giá trị x của A với giá trị của x thỏa mãn |2x-1|=3
c) Tìm x để (3-4x).A<3
d) Tìm giá trị nhỏ nhất của biểu thức B=(8-\(^{x^3}\)).A+x
Bài 8 :
1 . Tìm giá trị lớn nhất của các biểu thức .
a. B = - ( x + 18/1273 ) - 183/124 .
b. C = 15/( x - 8)² + 4 .
2 . Tìm các giá trị của x để các biểu thức sau nhận giá trị dương .
a. A = x² + 6 .
b. B = ( 5 - x ) . ( x + 8 ) .
c. C = ( x - 1 ) . ( x - 2 ) / x - 3 .
Bài 2:
a) \(A=x^2+6\ge6>0\forall x\in R\)
b) \(B=\left(5-x\right)\left(x+8\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}5-x>0\\x+8>0\end{matrix}\right.\\\left\{{}\begin{matrix}5-x< 0\\x+8< 0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}5>x\ge-8\left(nhận\right)\\-8>x>5\left(VLý\right)\end{matrix}\right.\)
Tính rồi so sánh giá trị của hai biểu thức (theo mẫu).
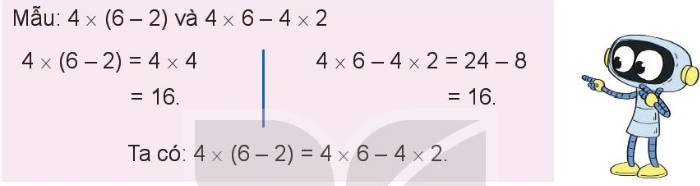
a) 23 x (7 - 4) và 23 x 7 - 23 x 4
b) (8 - 3) x 9 và 8 x 9 - 3 x 9
a,
23 x (7 - 4) = 23 x 3 = 69
23 x 7 - 23 x 4 = 161 - 92 = 69
Ta có: 23 x (7 - 4) = 23 x 7 - 23 x 4
b,
(8 - 3) x 9 = 5 x 9 = 45
8 x 9 - 3 x 9 = 72 - 27 = 45
Ta có: (8 - 3) x 9 = 8 x 9 - 3 x 9
1)Giai phương trình
a) (2\(\sqrt{x}\)+3)(\(\sqrt{x}\)-1)-5= 2x-4
b) x\(\sqrt{x}\)-8 = 3\(\sqrt{x}\) (\(\sqrt{x}\)-2)
2) Cho biểu thức: M= 2y-3x\(\sqrt{y}\) + x2
a) Phân tích M thành nhân tử
b) Tính giá trị M khi x = 2; y= \(\dfrac{18}{4+\sqrt{7}}\)
2
\(M=2y-3x\sqrt{y}+x^2=y-2x\sqrt{y}+x^2+y-x\sqrt{y}\\ =\left(\sqrt{y}-x\right)^2+\sqrt{y}\left(\sqrt{y}-x\right)\\ =\left(\sqrt{y}-x\right)\left(\sqrt{y}-x+\sqrt{y}\right)\\ =\left(\sqrt{y}-x\right)\left(2\sqrt{y}-x\right)\)
b
\(y=\dfrac{18}{4+\sqrt{7}}=\dfrac{18\left(4-\sqrt{7}\right)}{16-7}=\dfrac{72-18\sqrt{7}}{9}=\dfrac{72}{9}-\dfrac{18\sqrt{7}}{9}=8-2\sqrt{7}\\ =7-2\sqrt{7}.1+1=\left(\sqrt{7}-1\right)^2\)
Thế x = 2 và y = \(\left(\sqrt{7}-1\right)^2\) vào M được:
\(M=2\left(\sqrt{7}-1\right)^2-3.2.\sqrt{\left(\sqrt{7}-1\right)^2}+2^2\\ =2\left(8-2\sqrt{7}\right)-6.\left(\sqrt{7}-1\right)+4\\ =16-4\sqrt{7}-6\sqrt{7}+6+4\\ =26-10\sqrt{7}\)
1:
a: =>2x-2căn x+3căn x-3-5=2x-4
=>căn x-8=-4
=>căn x=4
=>x=16
b: \(\Leftrightarrow\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)-3\sqrt{x}\left(\sqrt{x}-2\right)=0\)
=>(căn x-2)(x-căn x+4)=0
=>căn x-2=0
=>x=4