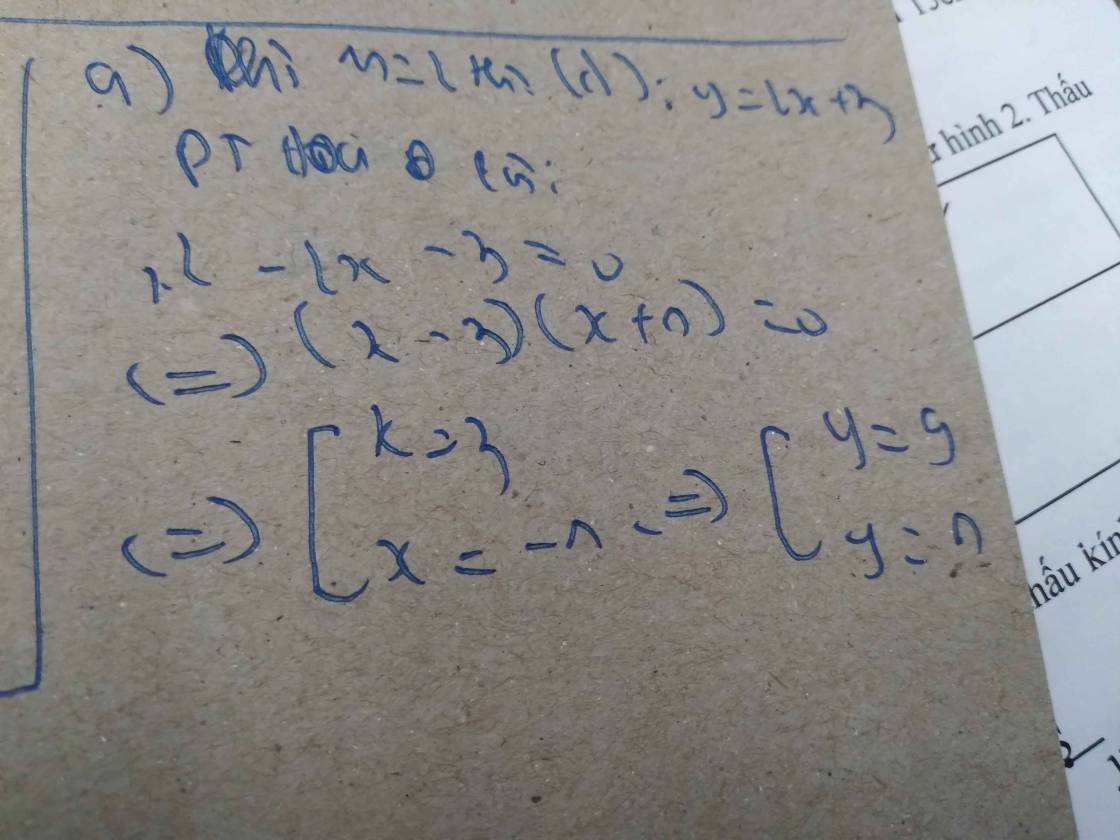tọa độ giao đr của 2 đt y=x-1 và y= -x+2 là:

Những câu hỏi liên quan
Bài 5: a) Vẽ đt các hs sau trên cùng mặt phẳng tọa độ: y = 2x (1); y = 0,5x (2); y = - x + 6 (3) b) Gọi các giao điểm của các đt có pt (3) với 2 đt có pt (1) và (2) theo thứ tự là A và B. Tìm tọa độ của 2 điểm A và B c) Tính các góc của tam giác OAB
b: Phương trình hoành độ giao điểm của (3) và (1) là:
2x=-x+6
hay x=2
Thay x=2 vào (1), ta được:
\(y=2\cdot2=4\)
Vậy: A(2;4)
Phương trình hoành độ giao điểm của (3) và (2) là:
-x+6=0.5x
\(\Leftrightarrow-1.5x=-6\)
hay x=4
Thay x=4 vào y=-x+6, ta được:
y=6-4=2
Vậy: A(4;2)
Đúng 1
Bình luận (0)
cho điểm A(-1;2) đt Delta 2x - y-1 0 và đtròn ( c) (x-1)^2 + (y-2)^29tìm tọa độ giao điểm a1 là ảnh của a qua Đoxtìm tọa độ điểm a2 là ảnh của a qua Đoyviết pt đt Delta^, là ảnh của Delta qua Đoxviết pt đtron ( c^,) là ảnh của (c) qua Đoygiải nhanh giúp mình với
Đọc tiếp
cho điểm A(-1;2) đt \(\Delta\) 2x - y-1 =0 và đtròn ( c) (x-1)\(^2\) + (y-2)\(^2\)=9
tìm tọa độ giao điểm a1 là ảnh của a qua Đox
tìm tọa độ điểm a2 là ảnh của a qua Đoy
viết pt đt \(\Delta^,\) là ảnh của \(\Delta\) qua Đox
viết pt đtron ( c\(^,\)) là ảnh của (c) qua Đoy
giải nhanh giúp mình với
a: Tọa độ A1 là ảnh của A qua phép đối xứng trục Ox là:
\(\left\{{}\begin{matrix}x_{A_1}=x_A=-1\\y_{A_1}=-y_A=-2\end{matrix}\right.\)
Vậy: \(A_1\left(-1;-2\right)\)
b: Tọa độ A2 là ảnh của A qua phép đối xứng trục Oy là:
\(\left\{{}\begin{matrix}x_{A_2}=-x_A=1\\y_{A_2}=y_A=2\end{matrix}\right.\)
Vậy: \(A_2\left(1;2\right)\)
c: Tọa độ giao điểm B của (Δ) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\2x-y-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=0\end{matrix}\right.\)
Vậy: B(1/2;0)
Vì B thuộc Ox nên phép đối xứng qua trục Ox biến B thành chính nó
Lấy C(1;1) thuộc (d)
Tọa độ D là ảnh của C qua phép đối xứng trục Ox là:
\(\left\{{}\begin{matrix}x_D=x_C=1\\y_D=-y_C=-1\end{matrix}\right.\)
Vậy: D(1;-1)
Do đó: Δ' là phương trình đường thẳng đi qua hai điểm B(1/2;0); D(1;-1)
\(\overrightarrow{BD}=\left(\dfrac{1}{2};-1\right)=\left(1;-2\right)\)
=>VTPT là (2;1)
Phương trình Δ' là:
\(2\left(x-1\right)+1\left(y+1\right)=0\)
=>2x-2+y+1=0
=>2x+y-1=0
Đúng 2
Bình luận (0)
cho đthẳng yaxb (a≠0) (d)a) Xác định đt (d) biết (d) đi qua 2 điểm A(1;-2) và B(-2;3)b)vẽ đt (d) tìm được ở câu a và đt (d) yx-3 trê cùng 1 mặt phẳng tọa độ.c) Gọi M là giao điểm của (d) và (d) tìm tọa độ giao điểm Md)gọi P;Q lần lượt là giao điểm của (d) và (d) với trục Oxd1) Tính góc MPQd2) tính chu vi và diện tích △MPQ
Đọc tiếp
cho đthẳng y=ax=b (a≠0) (d)
a) Xác định đt (d) biết (d) đi qua 2 điểm A(1;-2) và B(-2;3)
b)vẽ đt (d) tìm được ở câu a và đt (d') y=x-3 trê cùng
1 mặt phẳng tọa độ.
c) Gọi M là giao điểm của (d) và (d') tìm tọa độ giao điểm M
d)gọi P;Q lần lượt là giao điểm của (d) và (d') với trục Ox
d1) Tính góc MPQ
d2) tính chu vi và diện tích △MPQ
a, Từ giả thiết suy ra \(\left\{{}\begin{matrix}a+b=-2\\-2a+b=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=-\dfrac{1}{3}\end{matrix}\right.\Rightarrow y=-\dfrac{5}{3}x-\dfrac{1}{3}\)
b,
c, Phương trình hoành độ giao điểm
\(-\dfrac{5}{3}x-\dfrac{1}{3}=x-3\Leftrightarrow x=1\Rightarrow y=-2\Rightarrow M\left(1;-2\right)\)
d1, \(tanMPQ=-\left(-\dfrac{5}{3}\right)=\dfrac{5}{3}\Rightarrow\widehat{MPQ}\approx59^o\)
d2, \(P\left(-\dfrac{1}{5};0\right);Q\left(3;0\right);M\left(1;-2\right)\)
Chu vi \(P=PQ+QM+MP=\dfrac{16}{5}+2\sqrt{2}+\dfrac{2\sqrt{34}}{5}\)
\(p=\dfrac{\dfrac{16}{5}+2\sqrt{2}+\dfrac{2\sqrt{34}}{5}}{2}\)
Diện tích \(S=\sqrt{p\left(p-\dfrac{16}{5}\right)\left(p-2\sqrt{2}\right)\left(p-\dfrac{2\sqrt{34}}{5}\right)}=...\)
Đúng 1
Bình luận (0)
Cho (P): y=x2 và đt (d):y=(2m+1)x-2m-1.Tìm tọa độ giao điểm của (d) và (P) khi m=1/2
Xác định tọa độ giao điểm của đt (d) 4x-5y=9 và parabol y=-x
(P): y=-x^2
4x-5y=9
=>5y=4x-9
=>y=4/5x-9/5
PTHDGĐ là:
-x^2-4/5x+9/5=0
=>x=1 hoặc x=-9/5
=>y=1 hoặc y=81/25
Đúng 0
Bình luận (0)
cho hai đt (d): y=-2x+1
(d1) : y=x-1
a) vẽ đồ thị (d) và (d1) trên cùng mptđ
b) xác định tọa độ giao điểm A của 2 đt (d) và (D1) bằng phép toán
c) viết pt đường thẳng (d2): y=ax+b (\(a\ne0\)) song song với đt (D1) cắt trục hoành tại điểm có hoành độ bằng 2
a)( x= 0 ; y = 1); (y=0; x= 1/2) đt1
(x=0;y = -1) ; (y=0;x= 1) đt2
b) giao điểm tức là cùng nghiệm
-2x+1 = x- 1 => x = 2/3 ; y = -1/3
A(2/3; -1/3)
c) anh xem đk // là làm dc, em mệt r
Đúng 0
Bình luận (2)
(d):y=mx-m+1
(P):y=x^2
a) tìm tọa độ giao điểm của (d) và (P) khi m=4
b)tìm giá trị của m để đt (d) và (P) cắt nhau tại hai điểm phân biệt có hoành độ x1,x2 là độ dài 2 cạnh góc vuông của 1 tam giác có độ dài đường cao ứng với cạnh huyền bằng 1/√5
a) Xét pt hoành độ gđ của (d) và (P):
\(x^2-mx+m-1=0\) (*)
Thay m=4 vào pt (*) => x=3 và x=1 thay vào (P) suy ra được tung độ tương ứng y=9 và y=1
Đ/a: \(\left(3;9\right),\left(1;1\right)\)
b) Để (d) và (P) cắt nhau tại hai điểm pb <=> \(\Delta>0\) <=> \(m^2-4\left(m-1\right)>0\) <=> \(\left(m-2\right)^2>0\) <=> \(m\ne2\)
Theo giả thiết => \(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}=\dfrac{1}{\left(\dfrac{1}{\sqrt{5}}\right)^2}\) (Áp dụng hệ thức lượng trong tam giác vuông)
\(\Leftrightarrow\dfrac{x^2_1+x_2^2}{x_1^2.x_2^2}=5\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-5\left(x_1x_2\right)^2=0\)
\(\Leftrightarrow m^2-2\left(m-1\right)-5\left(m-1\right)^2=0\)
\(\Leftrightarrow-4m^2+8m-3=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=\dfrac{1}{2}\end{matrix}\right.\)
Vậy...
Đúng 1
Bình luận (0)
cho parabol (P) : y= x^2 và đt (d): y = mx+3 a, Tìm tọa đọ giao điểm của (P) và (d) khi m= 2
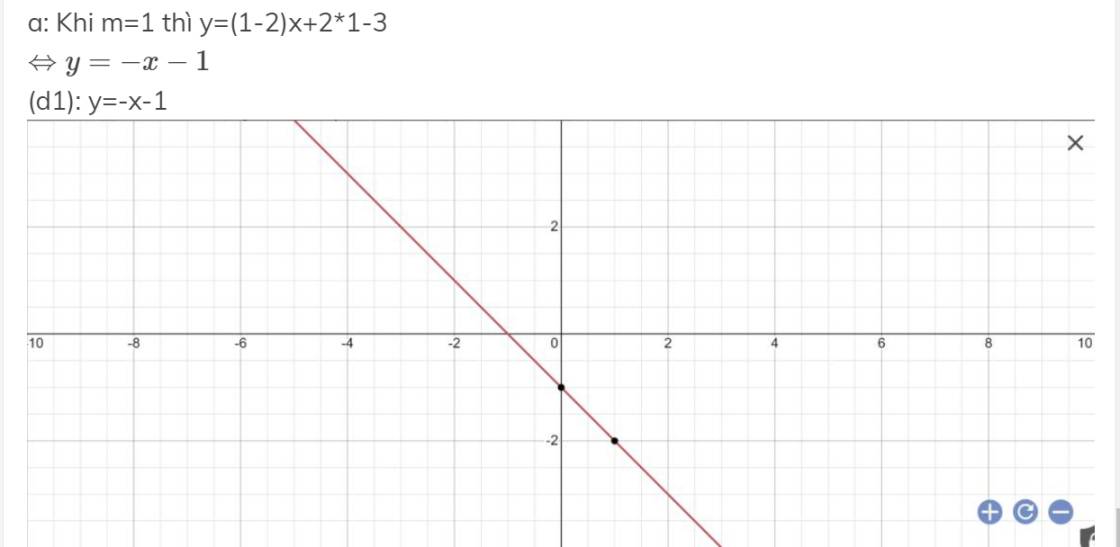
Cho đường thẳng (d): y= (m-2)x+2m-3
a) vẽ đồ thị của hàm số khi m=1. Gọi đt đó là (d1)
b) Cho (d2): y= x-5. Tìm tọa độ giao điểm A của (d1) và (d2)
c) c/m(d1) vuông góc với (d2), Tính chu vi tam giác tạo bởi (d1), (d2) và trục Oy