Những câu hỏi liên quan
Cho hình chóp S.ABCD , đáy ABCD là hình thang vuông tại A và D . SA vuông góc với (ABCD ) , AD=DC=AB/2=a , SA=a căn 3. Gọi I là trung điểm AB. CMR a. CI vuông góc (SAB ) , DI vuông góc (SAC) b. Các mặt bên hình chóp là những tam giác vuông
Cho hình chóp S.ABCD có đáy là hình thôi ABCD, góc \(\widehat{BAD}\) = 60 độ, cạnh SA vuông với mp đáy, SA=AB=a
a. CMR: BD vuông góc với mp(SAC)
b. Gọi H là trực tâm của tam giác SBD, M là trung điểm AD. Tính cosin của góc giữa (SB; (BHM)).
giúp mk câu b vs, mk ko bt vẽ trực tâm, cảm ơn
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB a, AD 2a, SA a. Tính thể tích khối chóp S.ABCD. A. 2a3 B. a3 C. a3/3 D. 2a3/3
Đọc tiếp
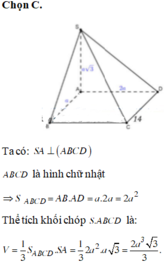
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a, SA =a. Tính thể tích khối chóp S.ABCD.
A. 2a3
B. a3
C. a3/3
D. 2a3/3
Đáp án D
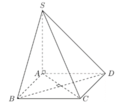
Diện tích hình chữ nhật ABCD là S = 2a2, chiều cao SA =a.
Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a,AD=2a Biết SA vuông góc với mặt phẳng đáy và SA=3a . Thể tích hình chóp S.ABCD là:
A. 6 a 3
B. 2 a 2
C. 2 a 3
D. a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD 2a. Biết SA vuông góc với mặt phẳng đáy và SA 3a. Thể tích hình chóp S.ABCD là: A.
6
a
3
B. 12
a
3
C. 2
a
3
D.
1
3
a
3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Biết SA vuông góc với mặt phẳng đáy và SA = 3a. Thể tích hình chóp S.ABCD là:
A. 6 a 3
B. 12 a 3
C. 2 a 3
D. 1 3 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, ABa, AD2a, SA vuông góc với mặt phẳng (ABCD),
S
A
a
3
. Thể tích của khối chóp S.ABCD là A.
2
a
3
3
B.
a
3
3
3
C.
2
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a, AD=2a, SA vuông góc với mặt phẳng (ABCD), S A = a 3 . Thể tích của khối chóp S.ABCD là
A. 2 a 3 3
B. a 3 3 3
C. 2 a 3 3 3
D. a 3 3
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, AD 2a, SA 2a, SA vuông góc với mp(ABCD). Tính thể tích khối chóp S.ABCD. A.
4
a
3
3
(đvtt) B.
4
a
3
(đvtt) C.
2
a
3
3
(đvtt) D.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, SA = 2a, SA vuông góc với mp(ABCD). Tính thể tích khối chóp S.ABCD.
A. 4 a 3 3 (đvtt)
B. 4 a 3 (đvtt)
C. 2 a 3 3 (đvtt)
D. 2 a 3 (đvtt)
Đáp án A
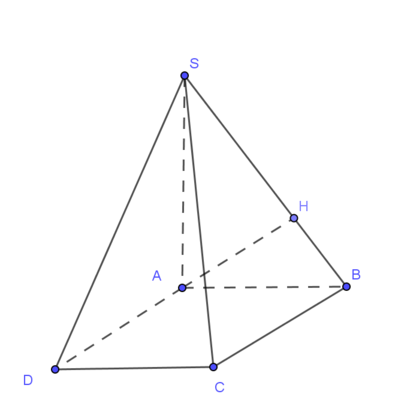
Ta có:
V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a .2 a = 4 3 a 3
Đúng 0
Bình luận (0)
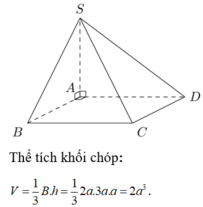
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 2a; AD 3a. Cạnh bên SA vuông góc với đáy ABCD và SA a. Tính thể tích V của khối chóp S.ABCD. A. V6a3 B. Va3 C. V3a3 D. V2a3.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a; AD = 3a. Cạnh bên SA vuông góc với đáy ABCD và SA = a. Tính thể tích V của khối chóp S.ABCD.
A. V=6a3
B. V=a3
C. V=3a3
D. V=2a3.
Cho hình chóp S.ABCD đáy là hình vuông, SA vuông góc với (ABCD) a) CMR : BC vuông góc với (SAB); CD vuông góc với (SAD) b) CMR : BD vuông góc với (SAC) c) Kẻ AE vuông góc với SB. CMR : SB vuông góc với (ADE)