giao điểm của parabol (P): y=4x2 với đường thẳng y=4 là \(A\left(x_1;y_1\right)\) và \(B\left(x_2;y_2\right)\). khi đó \(x_1y_2+x_2y_1=.......\)
Những câu hỏi liên quan
Trong mặt phẳng với hệ trục tọa đô, cho hai đường thẳng x+ y-1 0 và 3x –y+ 5 0. Hãy tìm diện tích hình bình hành có hai cạnh nằm trên hai đường thẳng đã cho, một đỉnh là giao điểm của hai đường thẳng đó và giao điểm của hai đường chéo là I(3;3). A. 74 B. 55 C. 54 D. 65.
Đọc tiếp
Trong mặt phẳng với hệ trục tọa đô, cho hai đường thẳng x+ y-1= 0 và 3x –y+ 5= 0. Hãy tìm diện tích hình bình hành có hai cạnh nằm trên hai đường thẳng đã cho, một đỉnh là giao điểm của hai đường thẳng đó và giao điểm của hai đường chéo là I(3;3).
A. 74
B. 55
C. 54
D. 65.
Đáp án B
Gọi hình bình hành là ABCD và
d:x+ y-1 = 0, ∆: 3x – y+ 5= 0 .
Không làm mất tính tổng quát giả sử
Ta có : 
. Vì I(3;3) là tâm hình bình hành nên C(7;4) ; 
=> Đường thẳng ACcó pt là: x- 4y + 9= 0.
Do 
=> Đường thẳng BC đi qua điểm C và có vtpt 
có pt là: 3x – y- 17= 0.
Khi đó :
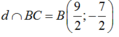
Ta có:
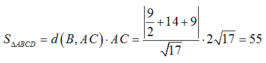
Đúng 0
Bình luận (0)
Cho đường thẳng y 2mx+3-m-x (d). Xác định m để :a, Đường thẳng d đi qua gốc tọa độb, Đường thẳng d song song với đường thẳng 2y-x 5c, Đường thẳng d tạo với Ox một góc nhọnd, Đường thẳng d tạo với Ox một góc tùe, Đường thẳng d cắt Ox tại điểm có hoành độ là 2f, Đường thẳng d cắt đồ thị hàm số y2x-3 tại một điểm có hoành độ là 2g, Đường thẳng d cắt đồ thị hàm số y -x+7 tại một điểm có tung độ y4h, Đường thẳng d đi qua giao điểm củ...
Đọc tiếp
Cho đường thẳng y= 2mx+3-m-x (d). Xác định m để :
a, Đường thẳng d đi qua gốc tọa độ
b, Đường thẳng d song song với đường thẳng 2y-x =5
c, Đường thẳng d tạo với Ox một góc nhọn
d, Đường thẳng d tạo với Ox một góc tù
e, Đường thẳng d cắt Ox tại điểm có hoành độ là 2
f, Đường thẳng d cắt đồ thị hàm số y=2x-3 tại một điểm có hoành độ là 2
g, Đường thẳng d cắt đồ thị hàm số y= -x+7 tại một điểm có tung độ y=4
h, Đường thẳng d đi qua giao điểm của 2 đường thẳng 2x-3y= -8 và y= -x+1
Cho hàm số y= -2x - 4 (d) và y= x +4 (d')
a) Vẽ đồ thị hai hàm số trên cùng mặt phẳng toạ độ ?
b) Gọi giao điểm của đường thẳng (d) và (d') với trục Oy lằn lượt là A;B và gọi giao điểm của hai ₫ường thẳng là C . Xác định toạ độ điểm C và tính diện tích tam giác ABC
c) Tính các góc của tam giác ABC
Đường thẳng (d) y = (m+1)x+3 cắt đường thẳng y = \(\dfrac{-3}{2}x+3\)
(d’) tại điểm M. Gọi N và P lần lượt là giao điểm của đường thẳng (d) và (d’) với trục hoành Ox. Tìm m để diện tích tam giác OMP bằng 2 lần diện tích tam giác OMN.
Cho tam giác ABC có AB = AC. Trên đường thẳng vuông góc với AC tại C lấy điểm D sao cho hai điểm B, D nằm khác phía đối với đường thẳng AC. Gọi K là giao điểm của đường thẳng qua B vuông góc với AB và đường thẳng qua trung điểm M của CD và vuông góc với AD. Chứng minh KB = KD.
Cho tam giác ABC có AB = AC. Trên đường thẳng vuông góc với AC tại C lấy điểm D sao cho hai điểm B, D nằm khác phía đối với đường thẳng AC. Gọi K là giao điểm của đường thẳng qua B vuông góc với AB và đường thẳng qua trung điểm M của CD và vuông góc với AD. Chứng minh KB = KD.
Khi đường thẳng
∆
:
y
x
+
2
m
cắt parabol
P
:
y
x
2
-
x
+
3
tại hai điểm phân biệt A,B thì tọa độ trung điểm I của đoạn thẳng AB là A.
I
1
;
2
m
+
1
B.
I...
Đọc tiếp
Khi đường thẳng ∆ : y = x + 2 m cắt parabol P : y = x 2 - x + 3 tại hai điểm phân biệt A,B thì tọa độ trung điểm I của đoạn thẳng AB là
A. I 1 ; 2 m + 1
B. I - 1 ; 2 m - 1
C. I 2 ; 4 m + 2
D. I - 2 ; 4 m - 2
Phương trình hoành độ giao điểm của ∆ và (P) là
x 2 - x + 3 = x + 2 m ⇔ x 2 - 2 x + 3 = 0 (*)
Giả sử A ( x A ; y A ) thì B x B ; y B là các nghiệm của phương trình (*).
Theo định lí Vi-ét ta có x A + x B = 2 .
Ta có y A = x A + 2 m , y B = x B + 2 m nên y A + y B = x A + x B + 4 m = 2 + 4 m .
Tọa độ trung điểm I của đoạn thẳng AB là I x A + x B 2 ; y A + y B 2 = I 1 ; 2 m + 1 .
Chọn A.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có góc A tù.Kẻ AH vuông góc với đường thẳng CD tại H.Kẻ đường thẳng AE vuông góc với đường thẳng BC tại E.Từ D vẽ đường thẳng song song với AE cắt đường thẳng BC tại K.a,CM:ADKE là hình chữ nhậtb,Gọi M và N thứ tự là trung điểm của AH và DH.Gọi giao điểm của đường thẳng AE và đường thẳng DC là Q.CM:QM vuông góc với ANc,Cho I là trực tâm của tam giác AHE.Đường thẳng AI cắt đường thẳng HE tại FCho AC10cm,HE8cm,IF...
Đọc tiếp
Cho hình bình hành ABCD có góc A tù.Kẻ AH vuông góc với đường thẳng CD tại H.Kẻ đường thẳng AE vuông góc với đường thẳng BC tại E.Từ D vẽ đường thẳng song song với AE cắt đường thẳng BC tại K.
a,CM:ADKE là hình chữ nhật
b,Gọi M và N thứ tự là trung điểm của AH và DH.Gọi giao điểm của đường thẳng AE và đường thẳng DC là Q.
CM:QM vuông góc với AN
c,Cho I là trực tâm của tam giác AHE.Đường thẳng AI cắt đường thẳng HE tại F
Cho AC=10cm,HE=8cm,IF=1cm
Tính diện tích của tam giác AHE.
Help me,c question"
Cho tam giác ABC. AM là đường trung tuyến, đường thẳng song song với BC cắt các đoạn thẳng AB,AC,AM lần lượt tại D,E,N. a)Chứng minh N là trung điểm DE.
b) Gọi S là giao điểm của BN vả AC,K là giao điểm của CN và AB. Chứng minh KS//BC.
a) VÌ DE//BC
SUY RA \(\frac{DN}{BM}=\frac{AN}{AM}\)VÀ \(\frac{NE}{MC}=\frac{AN}{AM}\)\(\Rightarrow\frac{DN}{BM}=\frac{NE}{MC}\)mà BM=MC(m là trung diểm) nên DN=NE
b) dễ thấy \(\frac{KN}{KC}=\frac{DN}{BC}\)VÀ\(\frac{SN}{SB}=\frac{NE}{BC}\)mà \(\frac{DN}{BC}=\frac{NE}{BC}\)(NE=DN)
\(\Rightarrow\frac{KN}{KC}=\frac{SN}{SB}\)áp dụng định lí talet ta suy ra KS//BC
Đúng 0
Bình luận (0)