Những câu hỏi liên quan
cho góc xoy khác góc bẹt, trên cạnh ox, oy lấy các điểm a,b sao cho oa=ob. tia p/g của xoy cắt ab ở c.giác của góc xoy cat ab ở c. c/m ab vuông góc oc
Cho đường tròn (C) nằm trong góc xOy(đường tròn không có điểm chung với các cạnh góc xOy).
a) Hãy tìm trên (C) một điểm M sao cho tổng các khoảng cách từ M đến hai đường thẳng chứa cạnh của góc xOy là nhỏ nhất
b) Trên mặt phẳng xOy , vẽ đường tròn tâm C(3;4), R=2. Tính giá trị nhỏ nhất của tổng các khoảng cách từ M trên đường tròn (C) nói trên đến Ox và Oy
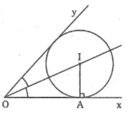
Cho góc xOy khác góc bẹt, điểm A nằm trên tia Ox. Dựng đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy
* Phân tích
Giả sử đường tròn (I) dựng được thỏa mãn điều kiện bài toán
- Đường tròn (I) tiếp xúc với Ox và Oy nên điểm I nằm trên tia phân giác của góc xOy
- Đường tròn (I) tiếp xúc với Ox tại A nên I nằm trên đường vuông góc với Ox kẻ từ A
Vậy I là giao điểm của tia phân giác góc xOy và đường thẳng vuông góc với Ox tại A
* Cách dựng
- Dựng tia phân giác của góc xOy
- Dựng đường thẳng vuông góc với Ox tại A cắt tia phân giác của góc xOy tại I
- Dựng đường tròn (I; IA)
* Chứng minh
Ta có: Ox ⊥ IA tại A nên Ox là tiếp tuyến của (I)
I nằm trên tia phân giác của góc xOy nên I cách đều hai cạnh Ox, Oy. Khi đó khoảng cách từ I đến Oy bằng IA nên Oy cũng là tiếp tuyến của đường tròn (I).
Vậy đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy.
* Biện luận
Vì góc xOy nhỏ hơn 180 ° nên góc tạo bởi một cạnh của góc với tia phân giác là góc nhọn. Khi đó đường thẳng vuông góc với Ox tại A luôn cắt tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Cho góc nhọn xOy và điểm M nằm trong góc đó. Chứng minh rằng nếu M cách đều hai cạnh của góc xOy thì M nằm trên tia phân giác của góc này.
kko bbitbbits
Câu 44: _TH_Cho góc xOy , vẽ tia phân giác Ot của góc xOy . Trên tia Ot lấy điểm M bất kỳ,
từ điểm M vẽ các đường thẳng vuông góc với tia Ox tại A và tia Oy tại B .
= OMA OMB
| theo trường hợp | |
| A. cạnh - cạnh - cạnh. | B. góc - cạnh - góc. |
| C. cạnh - góc - cạnh. | D. cạnh huyền - góc nhọn. |
Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy. Điểm M cách đều hai cạnh của góc xOy và cách đều hai điểm A, B. Xác định vị trí điểm M A. Điểm M là giao điểm của tia phân giác góc (xOy) và đường trung trực của AB B. Điểm M là giao điểm của tia phân giác góc (xOy) và AB C. Điểm M là điểm bất kì thuộc tia phân giác của góc A D. Điểm M là điểm thuộc đường trung trực của AB
Đọc tiếp
Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy. Điểm M cách đều hai cạnh của góc xOy và cách đều hai điểm A, B. Xác định vị trí điểm M
A. Điểm M là giao điểm của tia phân giác góc (xOy) và đường trung trực của AB
B. Điểm M là giao điểm của tia phân giác góc (xOy) và AB
C. Điểm M là điểm bất kì thuộc tia phân giác của góc A
D. Điểm M là điểm thuộc đường trung trực của AB
8 tháng 5 2022 lúc 19:04
Trên một cạnh của góc xOy (góc xOy khác 180 độ) đặt các đoạn thẳng OA=5cm;OB=16cm, trên cạnh thứ hai của góc đó, đặt các đoạn thẳng OC=8cm, OD=10cm.
a, Vẽ hình ghi giả thuyết kết luận.
b, Chứng minh tam giác OCD đồng dạng với tam giác OAD
a:
| GT | góc xOy OA=5cm; OB=16cm; OC=8cm; OD=10cm |
| KL | ΔOBC đồng dạng với ΔOAD |
b: Xét ΔOCB và ΔOAD có
OC/OA=OB/OD
góc O chung
=>ΔOCB đồng dạng với ΔOAD
Đúng 0
Bình luận (0)
8 tháng 5 2022 lúc 14:18
Trên một cạnh của góc xOy (góc xOy khác 180 độ) đặt các đoạn thẳng OA=5cm;OB=16cm, trên cạnh thứ hai của góc đó, đặt các đoạn thẳng OC=8cm, OD=10cm.
a, Vẽ hình ghi giả thuyết kết luận.
b, Chứng minh tam giác OCD đồng dạng với tam giác OAD
8 tháng 5 2022 lúc 9:35
Trên một cạnh của góc xOy (góc xOy khác 180 độ) đặt các đoạn thẳng OA=5cm;OB=16cm, trên cạnh thứ hai của góc đó, đặt các đoạn thẳng OC=8cm, OD=10cm.
a, Vẽ hình ghi giả thuyết kết luận.
b, Chứng minh tam giác OCD đồng dạng với tam giác OAD
Cho góc xoy nhọn trên cạnh ox và oy lần lượt lấy điểm M và N sao cho. ON=OM.Tia phân giác của góc xoy cắt mn tại i a) CM OI vuông góc MN b) gọi p là hình chiếu N trên Oy,Q là giao điểm của NP với OI.CM MQ vuông góc với Ox c) giả sử góc xoy=60^ ON=OM=6 cm.Tính độ dài OQ