hàm số y= f(x)y=f(x)
hàm số đã cho nghiich biến trong khoảng nào dưới đây
(1;cộng *)
(1;5)
(1tru
Những câu hỏi liên quan
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
-
x
2
x
+
2
,
∀
x
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.
-
2
;...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 - x 2 x + 2 , ∀ x Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. - 2 ; + ∞
B. - ∞ ; - 2
C. (-2;1)
D. (0;1)
Cho hàm số yf’(x) liên tục và có đạo hàm trên
ℝ
đồ thj hàm số yf’(x) như hình vẽ bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.
-
∞
;
-
2
B.
-
1
;
1
C.
2
;
+
∞...
Đọc tiếp
Cho hàm số y=f’(x) liên tục và có đạo hàm trên ℝ đồ thj hàm số y=f’(x) như hình vẽ bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
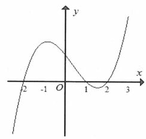
A. - ∞ ; - 2
B. - 1 ; 1
C. 2 ; + ∞
D. - ∞ ; - 1
Hàm số nghịch biến nếu f’(x)<0 Quan sát đồ thị y=f’(x), chọn đáp án A. Chọn A
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục và có đạo hàm trên R đồ thị hàm số yf(x) như hình vẽ bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Đọc tiếp
Cho hàm số y=f(x) liên tục và có đạo hàm trên R đồ thị hàm số y=f'(x) như hình vẽ bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
x
-
2
3
, với mọi x
∈
ℝ
. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (1;3) B. (-1;0) C. (0;1) D. (-2;0)
Đọc tiếp
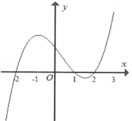
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x x - 2 3 , với mọi x ∈ ℝ . Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (1;3)
B. (-1;0)
C. (0;1)
D. (-2;0)
https://cdn.h.vn/bk/8N9Rgel5B18v.png
Cho hàm số yf(x) có đạo hàm liên tục trên
~
, hàm số yf’(x) có đồ thị hàm số như hình dưới đâyHàm số yf(x) đồng biến trên khoảng nào trong các khoảng sau: A. (-∞;2); (1;+∞) B. (-2;+∞)/{1} C. (-2;+∞) D. (-4;0)
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên ~ , hàm số y=f’(x) có đồ thị hàm số như hình dưới đây
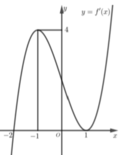
Hàm số y=f(x) đồng biến trên khoảng nào trong các khoảng sau:
A. (-∞;2); (1;+∞)
B. (-2;+∞)/{1}
C. (-2;+∞)
D. (-4;0)
Chọn C
Từ đồ thị hàm số y=f’(x) ta có bảng biến thiên cho hàm số y=f(x) như sau:
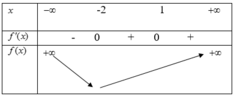
Nhìn vào bảng biến thiên ta thấy ngay trong khoảng (-2;+∞) thì hàm số y=f(x) đồng biến
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
(
x
-
1
)
(
x
-
4
)
g
(
x
)
, trong đó
g
(
x
)
0
,
∀
x
. Hàm số
y
f
(
x
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x - 4 ) g ( x ) , trong đó g ( x ) > 0 , ∀ x . Hàm số y = f ( x 2 ) đồng biến trên khoảng nào dưới đây?
A. ( - ∞ ; - 2 ) .
B. (-1;1).
C. (-2;-1).
D. (1;2).
Cho hàm số y=f(x) có bảng biến thiên
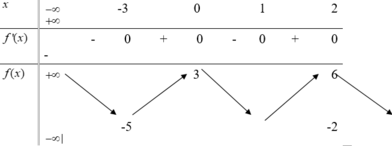
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (-5;3)
B. (-2;6)
C. (-3;1)
D. (1;2)
Dựa vào BBT hàm số đồng biến trên các khoảng (−3;0),(1;2).
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm f’(x) trên R. Hình vẽ bên là đồ thị của hàm số yf’(x). Hàm số
g
(
x
)
f
(
x
-
x
2
)
nghịch biến trên khoảng nào trong các khoảng dưới đây A.
-
∞
;
5
2
B.
3
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f’(x) trên R. Hình vẽ bên là đồ thị của hàm số y=f’(x). Hàm số g ( x ) = f ( x - x 2 ) nghịch biến trên khoảng nào trong các khoảng dưới đây
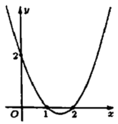
A. - ∞ ; 5 2
B. 3 2 ; + ∞
C. 1 2 ; + ∞
D. - ∞ ; 1 2
Cho hàm số yf(x). Hàm số yf(x) có đồ thị như hình bên. Hàm số
y
f
(
1
+
x
2
)
nghịch biến trên khoảng nào dưới đây? A.
(
3
;
+
∞
)
B.
(
-
3
;
-
1
)
C.
(
1
;...
Đọc tiếp
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng nào dưới đây?
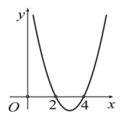
A. ( 3 ; + ∞ )
B. ( - 3 ; - 1 )
C. ( 1 ; 3 )
D. (0;1)
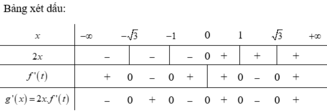
Vậy hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng ( 1 ; 3 )
Đúng 0
Bình luận (0)