\(=x\left(2x-7\right)-2\left(2x-7\right)=\left(x-2\right)\left(2x-7\right)\)

x(2x - 7) + 14 - 4x

= x(2x - 7) - 4x + 14

= x(2x - 7) - 2(2x - 7)

= (x - 2)(2x - 7)

\(x\cdot\left(2x-7\right)-4x+14=0\)

\(\Leftrightarrow x\cdot\left(2x-7\right)-2\cdot\left(2x-7\right)=0\)

\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\end{matrix}\right.\)

`x(2x-7)-4x+14=0`

`<=> 2x^2-7x-4x+14=0`

`<=> 2x^2-11x+14=0`

`<=> (2x^2-4x)-(7x-14)=0`

`<=>2x(x-2)-7(x-2)=0`

`<=>(2x-7)(x-2)=0`

`<=>` \(\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\end{matrix}\right.\)

Vậy `S={7/2 ; 2}`.

pt <=> 2x\(^2\)-7x-4x+14=0

<=> 2x\(^2\)-11x+14=0

<=> 2x\(^2\)-4x-7x+14=0

<=> (2x-7)(x-2)=0

<=> \(\left[{}\begin{matrix}x=2\\x=\dfrac{7}{2}\end{matrix}\right.\)

1) x³ - 4x² - 8x + 8 

Thử với x = -2 ta có : (-2)³ - 4.(-2)² - 8.(-2) + 8 = 0

Vậy -2 là nghiệm của đa thức . Theo hệ quả của định lí Bézout thì đa thức trên chia hết cho x + 2

Thực hiện phép chia x³ - 4x² - 8x + 8 cho x + 2 ta được x² - 6x + 4

=> x³ - 4x² - 8x + 8 = ( x + 2 )( x² - 6x + 4 )

2) 3x² + 13x - 10

= 3x² + 15x - 2x - 10

= 3x( x + 5 ) - 2( x + 5 )

= ( x + 5 )( 3x - 2 )

3) x( 2x - 7 ) - 7 - 4x + 14 = 0

<=> 2x² - 7x - 4x + 7 = 0

<=> 2x² - 11x + 7 = 0

<=> 2( x² - 11/2x + 121/16 ) - 65/8 = 0

<=> 2( x - 11/4 )² = 65/8

<=> ( x - 11/4 )² = 65/16

<=> ( x - 11/4 )² = \(\left(\pm\sqrt{\frac{65}{16}}\right)^2=\left(\pm\frac{\sqrt{65}}{4}\right)^2\)

<=> \(\orbr{\begin{cases}x-\frac{11}{4}=\frac{\sqrt{65}}{4}\\x-\frac{11}{4}=\frac{-\sqrt{65}}{4}\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{11+\sqrt{65}}{4}\\x=\frac{11-\sqrt{65}}{4}\end{cases}}\)

4) 2x³ + 3x² + 2x + 2 = 0 ( chịu không làm được ((: )

\(x\left(2x-7\right)-4x+14=0\)

\(\Leftrightarrow x\left(2x-7\right)-2\left(2x-7\right)=0\)

\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\end{matrix}\right.\)

Vậy ................

a) ( x + 2 )( 3 - 4x ) = x² + 4x + 4

<=> ( x + 2 )( 3 - 4x ) = ( x + 2 )²

<=> 3 - 4x = x + 2

<=> -4x - x = 2 - 3

<=> -5x = -1

<=> x = \(\frac{1}{5}\)

b) x(2x - 7) - 4x + 14 = 0

<=> x(2x - 7) = 4x - 14

<=> x(2x - 7) = 2(2x - 7)

<=> x = 2

c) 3x - 15 = 2x(x - 5)

<=> 3(x - 5) = 2x(x - 5)

<=> 3 = 2x

<=> x = \(\frac{3}{2}\)

d) (2x + 1)(3x - 2) = (5x - 8)(2x + 1)

<=> 3x - 2 = 5x - 8

<=> 3x - 5x = -8 + 2

<=> -2x = -6

<=> x = 3

mk ko bt 123

Suy ra (2x-4)-(3x-3×5)=1 Suy ra(2x-4)-3x+15=1 Suy ra 2x-4-3x+15=1 Suy ra (2x-3x)+(15-4)=1 -1x+11=1 1-11=-1x -1x=-10 X=10

x-3)^2-2(2x-7)(x-3)=0

Trả lời 

x(2x-7)+(14-4x)=0

=> 2x² - 7x + 14 - 4x = 0

=> 2x² - 11x + 14 = 0

Giải phương trình trên máy tính ta có 

X₁ = \(\frac{7}{2}\)

X₂ = 2

Vậy X = \(\frac{7}{2}\)hoặc X = 2

Study well 

\(x\left(2x-7\right)+\left(14-4x\right)=0\)

\(\Leftrightarrow2x^2-7x+14-4x=0\)

\(\Leftrightarrow2x^2-11x+14=0\)

\(\Leftrightarrow2x^2-4x-7x+14=0\)

\(\Leftrightarrow2x\left(x-2\right)-7\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(2x-7\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\2x-7=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=\frac{7}{2}\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=2\\x=\frac{7}{2}\end{cases}}\)

a ) \(5x+4=2x+13\)

\(\Leftrightarrow5x-2x=13-4\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\)

Vậy tập nghiệm của phương trình là S = {3}

b ) \(\left(x+2\right)\left(x-7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x-7=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=7\end{matrix}\right.\)

Vậy tập nghiệm của phương trình là \(S=\left\{-2;7\right\}\)

c ) \(\left|x-2\right|=2x+14\) ( 1 )

+ ) \(\left|x-2\right|=x-2\). Khi \(x-5\ge0\Leftrightarrow x\ge5\)

\(\left(1\right)\Leftrightarrow x-2=2x+14\)

\(\Leftrightarrow x-2x=14+2\)

\(\Leftrightarrow-x=16\Leftrightarrow x=-16\) ( Loại )

+ ) \(\left|x-5\right|=-x+5.\) Khi \(x-5< 0\Leftrightarrow x< 5\)

\(\left(1\right)\Leftrightarrow-x+2=2x+14\)

\(\Leftrightarrow-3x=12\)

\(\Leftrightarrow x=-4\) ( Thõa mãn )

Vậy ................

d ) \(4x-7< 17-2x\)

\(\Leftrightarrow4x+2x< 17+7\)

\(\Leftrightarrow6x< 24\)

\(\Leftrightarrow x< 4\)

Vậy ........

a) 5x + 4 = 2x +13

<=> 5x - 2x = 13- 4

<=> 3x = 9

<=> x = 3

Vậy phương trình có tập nghiệm S = { 3 }

b) (x+2). (x-7) = 0

=> \(\left[{}\begin{matrix}x+2=0\\x-7=0\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}x=-2\\x=7\end{matrix}\right.\)

Vậy phương trình có tập nghiệm S= { -2;7}

c)

khi x \(\ge\) 2 thì\(\left|x-2\right|\) = x - 2 khi đó phương trình có dạng :

x - 2 = 2x + 14

<=> x - 2x = 14+2

<=> -x = 16

<=> -x. (-1)= 16. (-1)

<=> x = -16 (loại )

khi x < 2 thì \(\left|x-2\right|\) = -x + 2 khi đó phương trình có dạng :

-x + 2 = 2x + 14

<=> -x - 2x = 14-2

<=> -3x = 12

<=> x = -4 (nhận)

Vậy phương trình có tập nghiệm S= { -4 }

x(2x – 7) – 4x + 14 = 0

ó x(2x – 7) – 2(2x – 7) = 0

ó (2x – 7)(x – 2) = 0

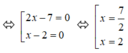
Vậy x = 7 2   hoặc x = 2

Đáp án cần chọn là: C